题目内容
已知点 ,直线
,直线 ,在直线
,在直线 上找一点
上找一点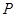 使得
使得 最小,则这个最小值为( )
最小,则这个最小值为( )
A. | B.8 | C.9 | D.10 |
D
解析试题分析:根据题意,由于点 ,在直线
,在直线 的同侧,则求解点A关于直线l的对称点A’(4,2),则可知A’B之间的距离即为使得
的同侧,则求解点A关于直线l的对称点A’(4,2),则可知A’B之间的距离即为使得 最小的值,这个最小值为10,故选D.
最小的值,这个最小值为10,故选D.
考点:两点距离的最值
点评:解决的关键是利用对称性,将同侧的一点关于直线对称后,与另一个点的连线即为所求。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
直线l经过原点和点(-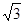 , 1),则它的斜率为
, 1),则它的斜率为
A.-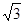 | B.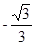 | C.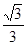 | D.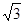 |
无论 为何实值,直线
为何实值,直线 总过一个定点,该定点坐标为( ).
总过一个定点,该定点坐标为( ).
A.(1, ) ) | B.( , , ) ) | C.( , , ) ) | D.( , , ) ) |
已知直线 过点
过点 ,且在两坐标轴上的截距互为相反数,则直线
,且在两坐标轴上的截距互为相反数,则直线 的方程为( )
的方程为( )
A. |
B. 或 或 |
C. 或 或 |
D. 或 或 |
已知点 的坐标满足条件
的坐标满足条件 则点
则点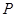 到直线
到直线 的距离的最小值为( )
的距离的最小值为( )
A. | B. | C. | D. |
若直线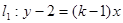 和直线
和直线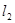 关于直线
关于直线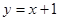 对称,那么直线
对称,那么直线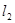 恒过定点( )
恒过定点( )
| A.(2,0) | B.(1,-1) | C.(1,1) | D.(-2,0) |
已知直线 ,
, ,若
,若 ∥
∥ ,则
,则 的值是( )
的值是( )
A. | B. | C. 或1 或1 | D.1 |
已知 ,则
,则 的边
的边 上的中线所在的直线方程为( )
上的中线所在的直线方程为( )
A. | B. | C. | D. |
直线 的倾斜角是( )
的倾斜角是( )
| A.30° | B.120° | C.60° | D.150° |