题目内容
已知点A（1+sin（
-2x），1），B（1，
sin（π-2x）+a）（x∈R，a），y=
•
．
（1）求y关于x的函数关系式y=f（x）；
（2）当x∈[0，
]时f（x）的最大值为4，求a的值．
| π |
| 2 |
| 3 |
| OA |
| OB |
（1）求y关于x的函数关系式y=f（x）；
（2）当x∈[0，
| π |
| 3 |
∵（1）点A（1+sin（
-2x），1），B（1，
sin（π-2x）+a）（a、x∈R，），
∴y=f（x）=
•
=（1+sin（
-2x），1）•（1，
sin（π-2x）+a）=1+cos2x+
sin2x+a=2sin（
+2x）+a+1
（2）当x∈[0，
]时，
≤2x+
≤
，故当2x+
=
时，函数y有最大值等于2+a+1=4，a=1．
| π |
| 2 |
| 3 |
∴y=f（x）=
| OA |
| OB |
| π |
| 2 |
| 3 |
| 3 |
| π |
| 6 |
（2）当x∈[0，
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| π |
| 2 |
练习册系列答案
相关题目
-2x），1），B（1，
sin（π-2x）+a）（x∈R，a），y=
．
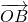]时f（x）的最大值为4，求a的值．
-2x），1），B（1，
sin（π-2x）+a）（x∈R，a），y=
．
]时f（x）的最大值为4，求a的值．