题目内容
根据程序设定,机器人在平面上能完成下列动作:从原点O出发,以匀速v(m/s)沿东偏北α(α为(0, )内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 .
)内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 .
【答案】分析:设改变方向的点为M,过M作x轴的垂线,垂足为N,根据速度和时间求出|OM|+|PM|的长,在△OPM中然后根据三角形的两边之和大于第三边列出一个不等式,然后在△OMN中,根据两边之和大于第三边列出另外一个不等式,然后再根据x≥0,y≥0,在平面直角坐标系中画出相应的平面区域为一个弓形,利用四分之一圆的面积减去等腰直角三角形的面积即可求出弓形的面积.
解答:解:设改变方向的点位M,则OM+MP=vt
△OPM中,OM+MP≥OP(O,M,P共线时取等号)
∴OP≤vt即x2+y2≤(vt)2
△OMN中,OM≤ON+MN(O,M,N三点共线时取等号)
∴OM+MP≤ON+MN+MP=x+y
即vt≤x+y
机器人行走t(s)时的可能落点P的区域为Ω,则 ,所表示的平面区域为(1)中的弓形
,所表示的平面区域为(1)中的弓形
∴面积S= =
=
∴
故答案为:
(1)

(2)

点评:此题考查学生会进行简单的线性规划,解题的关键是准确找出x,y满足的条件,考查了数形结合的数学思想,是一道综合题.
解答:解:设改变方向的点位M,则OM+MP=vt
△OPM中,OM+MP≥OP(O,M,P共线时取等号)
∴OP≤vt即x2+y2≤(vt)2
△OMN中,OM≤ON+MN(O,M,N三点共线时取等号)
∴OM+MP≤ON+MN+MP=x+y
即vt≤x+y
机器人行走t(s)时的可能落点P的区域为Ω,则
 ,所表示的平面区域为(1)中的弓形
,所表示的平面区域为(1)中的弓形∴面积S=
 =
=
∴

故答案为:

(1)

(2)

点评:此题考查学生会进行简单的线性规划,解题的关键是准确找出x,y满足的条件,考查了数形结合的数学思想,是一道综合题.

练习册系列答案
相关题目
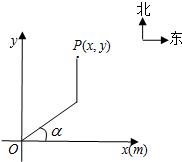 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
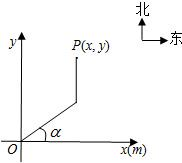 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α( )方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )
)方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )