题目内容
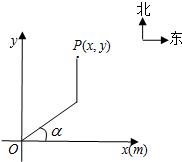 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(0≤α≤| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:我们不妨令机器人在M点改变方向,由三角形的性质,我们易得到:|OM|+|MP|=2×10=20≥|OP|=
,及|OM|+|MP|≤|ON|+|NM|+|MP|=x+y,由此我们易得x,y满足的约束条件,得到答案.
| x2+y2 |
解答: 解:设改变方向的点为M,
解:设改变方向的点为M,
依题意|OM|+|MP|=10×2=20米
△OPM中,|OM|+|MP|≥|OP|(当O、M、P共线时“=”成立)
∴|OP|≤20,即x2+y2≤400
又△OMN中,|OM|≤|ON|+|NM|(当O、M、N共线时“=”成立)
∴|OM|+|MP|≤|ON|+|NM|+|MP|=x+y
∴x+y≥20
故选:B
 解:设改变方向的点为M,
解:设改变方向的点为M,依题意|OM|+|MP|=10×2=20米
△OPM中,|OM|+|MP|≥|OP|(当O、M、P共线时“=”成立)
∴|OP|≤20,即x2+y2≤400
又△OMN中,|OM|≤|ON|+|NM|(当O、M、N共线时“=”成立)
∴|OM|+|MP|≤|ON|+|NM|+|MP|=x+y
∴x+y≥20
故选:B
点评:本题考查的知识点是二元一次不等式(组)与平面区域,根据三角形的性质,判断边与边之间的关键是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
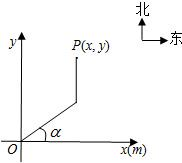 根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α(
根据程序设定,机器人在平面上能完成下列动作:先从原点O沿正东偏北α( )内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 .
)内的变量)方向或正北方向行走,且方向改变的时间不定.记机器人行走t(s)时的可能落点P的区域为Ω,则Ω的面积与(vt)2的比值为 . )方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )
)方向行走一段时间后,再向正北方向行走一段时间,但α的大小以及何时改变方向不定.如图.假定机器人行走速度为10米/分钟,设机器人行走2分钟时的可能落点区域为S,则S的面积(单位:平方米)等于( )