题目内容
已知曲线C1:x2+y2=1,对它先作矩阵A=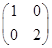 对应的变换,再作矩阵B=
对应的变换,再作矩阵B= 对应的变换得到曲线C2:
对应的变换得到曲线C2: +y2=1,求实数b的值.
+y2=1,求实数b的值.
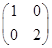 对应的变换,再作矩阵B=
对应的变换,再作矩阵B= 对应的变换得到曲线C2:
对应的变换得到曲线C2: +y2=1,求实数b的值.
+y2=1,求实数b的值.b=±1
从曲线C1变到曲线C2的变换对应的矩阵BA= =
= ,
,
在曲线C1上任意选一点P(x0,y0),设它在矩阵BA对应的变换作用下变为P'(x',y'),
则有 =
= ,
,
故
解得
代入曲线C1方程得,y'2+( x')2=1,
x')2=1,
即曲线C2方程为:( x)2+y2=1,
x)2+y2=1,
与已知的曲线C2的方程: +y2=1比较得(2b)2=4,
+y2=1比较得(2b)2=4,
所以b=±1.
 =
= ,
,在曲线C1上任意选一点P(x0,y0),设它在矩阵BA对应的变换作用下变为P'(x',y'),
则有
 =
= ,
,故

解得

代入曲线C1方程得,y'2+(
 x')2=1,
x')2=1,即曲线C2方程为:(
 x)2+y2=1,
x)2+y2=1,与已知的曲线C2的方程:
 +y2=1比较得(2b)2=4,
+y2=1比较得(2b)2=4,所以b=±1.

练习册系列答案
相关题目
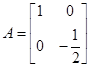 ,则矩阵A的逆矩阵为
,则矩阵A的逆矩阵为  +
+ =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程. ,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程.
,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程. =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程. ,矩阵运算
,矩阵运算 都成立,则
都成立,则 .
. =
= ,变换T的矩阵为A=
,变换T的矩阵为A= ,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1
,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1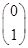 =
=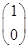 ,M
,M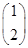 =
=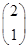 ,求M2.
,求M2. 之下的对应点的坐标为(-2,-4),求m、k的值.
之下的对应点的坐标为(-2,-4),求m、k的值.