题目内容
设抛物线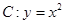 ,
,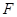 为焦点,
为焦点,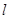 为准线,准线与
为准线,准线与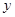 轴交点为
轴交点为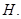
(1)求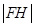 ;
;
(2)过点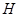 的直线与抛物线
的直线与抛物线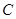 交于
交于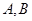 两点,直线
两点,直线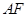 与抛物线交于点
与抛物线交于点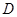 .
.
①设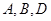 三点的横坐标分别为
三点的横坐标分别为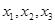 ,计算:
,计算: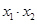 及
及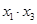 的值;
的值;
②若直线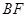 与抛物线交于点
与抛物线交于点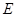 ,求证:
,求证: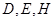 三点共线.
三点共线.
(1)  (2)
(2)  ,
, ,并根据斜率相等来证明三点共线。
,并根据斜率相等来证明三点共线。
解析试题分析:(1)
(2)设直线 方程:
方程: ,直线
,直线 方程:
方程:






设


 三点共线。
三点共线。
考点:直线与抛物线的位置关系
点评:解决的关键是利用抛物线的定义,以及联立方程组的思想来得到根与系数的关系,结合点的坐标来求解斜率,确定点的位置,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的直线
的直线 交直线
交直线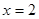 于
于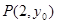 ,过点
,过点 的直线
的直线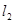 交
交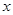 轴于
轴于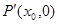 点,
点,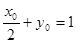 ,
,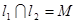 .
.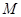 的轨迹
的轨迹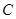 的方程;
的方程;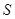 、
、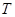 ,已知点
,已知点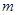 )在线段
)在线段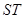 的垂直平分线上且
的垂直平分线上且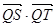 ≤4,求实数
≤4,求实数 O
O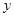 中,直线
中,直线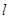 与抛物线
与抛物线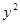 =2
=2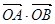 =3”是真命题;
=3”是真命题;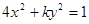 的曲线是焦点在
的曲线是焦点在 上的椭圆 ,求
上的椭圆 ,求 的取值范围
的取值范围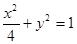 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.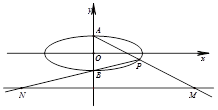
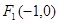 及
及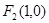 ,点
,点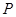 在以
在以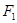 、
、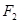 为焦点的椭圆
为焦点的椭圆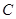 上,且
上,且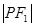 、
、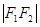 、
、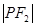 构成等差数列.
构成等差数列.
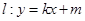 与椭圆
与椭圆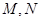 是直线
是直线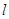 上的两点,且
上的两点,且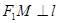 ,
,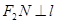 . 求四边形
. 求四边形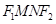 面积
面积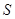 的最大值.
的最大值.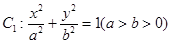 的右焦点
的右焦点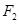 与抛物线
与抛物线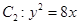 的焦点重合,左端点为
的焦点重合,左端点为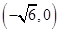
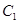 的右焦点且斜率为
的右焦点且斜率为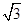 的直线
的直线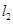 被椭圆
被椭圆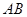 。
。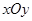 中,以
中,以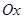 轴为始边作两个锐角
轴为始边作两个锐角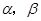 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于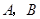 两点.已知
两点.已知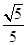 ,
,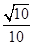 .
.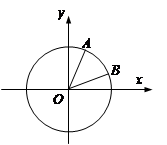
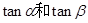 的值;(2)求
的值;(2)求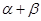 的值.
的值.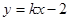 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.