题目内容
已知α为第二象限角,cosα=-
,则tan2α的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
分析:依题意,可求得sinα=
,tanα=
=-
,利用二倍角的正切即可求得tan2α的值.
| 4 |
| 5 |
| sinα |
| cosα |
| 4 |
| 3 |
解答:解:∵α为第二象限角,cosα=-
,
∴sinα=
=
=
,
∴tanα=
=-
,
∴tan2α=
=
=
,
故选:B.
| 3 |
| 5 |
∴sinα=
| 1-cos2α |
1-(-
|
| 4 |
| 5 |
∴tanα=
| sinα |
| cosα |
| 4 |
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
2×(-
| ||
1-(-
|
| 24 |
| 7 |
故选:B.
点评:本题考查同角三角函数间的关系式的应用,着重考查二倍角的正切,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求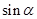 和
和 及
及 的值.
的值.