题目内容
3.设{an}是公比不为1的等比数列,且a5,a3,a4成等差数列,求数列{an}的公比.分析 利用等比数列的通项公式和等差数列的性质求解.
解答 解:∵{an}是公比不为1的等比数列,且a5,a3,a4成等差数列,
∴2${a}_{1}{q}^{2}$=${a}_{1}{q}^{4}+{a}_{1}{q}^{3}$,
∴q2+q-2=0,
解得q=-2或q=1.
∴数列{an}的公比为-2.
点评 本题考查等比数列的公比的求法,是基础题,解题时要认真审题,注意等比数列和等差数列的性质的合理运用.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.已知双曲线C:${x^2}-\frac{y^2}{3}=1$的左、右焦点分别是F1,F2,若A是双曲线右支上一点且满足$∠{F_1}A{F_2}={60^o}$,则${S_{△{F_1}A{F_2}}}$=( )
| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
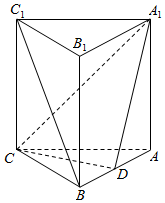 已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点
已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点