题目内容
已知函数f(x)是奇函数，函数φ(x)是偶函数，定义域x∈{x|x∈R,x≠
+
,k∈Z},且f(x)+φ(x)=tan(x+
).求f(x)和φ(x)的解析式.
解:因为f(x)是奇函数，φ(x)是偶函数.
∴f(-x)=-f(x),φ(-x)=φ(x).
∵f(x)+φ(x)=tan(x+)=,①
∴f(-x)+φ(-x)=tan(-x+)=.
即-f(x)+φ(x)= 
.②
①+②得：2φ(x)=
+
,
∴φ(x)=
=
=
=
=sec2x.
①-②得:
-
,
∴f(x)=
=tan2x.
练习册系列答案
教学练新同步练习系列答案
相关题目
是奇函数，
)，当x∈(-4，-2)时，f(x)的最大值为-4．
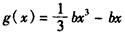，x∈(1，2)，若对任意的x1∈(1，2)，总存在x2∈(1，2)，使f(x1)-g(x2)=0，求实数b的取值范围． 
是奇函数，