题目内容
已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 在
在 上的最小值,并写出
上的最小值,并写出 取最小值时相应的
取最小值时相应的 值.
值.
 .
.(Ⅰ)求函数
 的最小正周期;
的最小正周期;(Ⅱ)求函数
 在
在 上的最小值,并写出
上的最小值,并写出 取最小值时相应的
取最小值时相应的 值.
值.(Ⅰ) ;(Ⅱ)
;(Ⅱ) 时,函数
时,函数 取得最小值
取得最小值
 ;(Ⅱ)
;(Ⅱ) 时,函数
时,函数 取得最小值
取得最小值
试题分析:(Ⅰ)先用正弦二倍角公式将角统一,再用化一公式,将
 整理成
整理成 的形式,根据正弦周期公式
的形式,根据正弦周期公式 求其周期。(Ⅱ)由(Ⅰ)知
求其周期。(Ⅱ)由(Ⅰ)知 ,根据
,根据 的范围,求整体角
的范围,求整体角 的范围,再根据正弦函数图像求
的范围,再根据正弦函数图像求 的范围,即可求得
的范围,即可求得 在
在 上的最小值及相应
上的最小值及相应 的值。
的值。试题解析:解:(Ⅰ)

 2分
2分 , 4分
, 4分所以函数
 的最小正周期
的最小正周期 6分
6分(Ⅱ)因为
 ,
, , 8分
, 8分 , 10分
, 10分 , 11分
, 11分所以当
 ,即
,即 时,函数
时,函数 取得最小值
取得最小值 . 13分
. 13分
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 的最小正周期为
的最小正周期为 .
. 的定义域;
的定义域; .
. 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 上的最大值和最小值,并求出相应的x的值.
上的最大值和最小值,并求出相应的x的值. .
. 的最小正周期;
的最小正周期; 则
则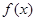 在区间[0,
在区间[0, ]上的最大值与最小值分别是( )
]上的最大值与最小值分别是( ) 在区间
在区间 上的最大值为3,则
上的最大值为3,则 = ;
= ; 在
在 上至少含有20个零点时,
上至少含有20个零点时, 的最小值为 .
的最小值为 . 的部分图像如图所示,设
的部分图像如图所示,设 为坐标原点,
为坐标原点, 是图像的最高点,
是图像的最高点, 是图像与
是图像与 轴的交点,则
轴的交点,则 的值为( )
的值为( )


 (
( )的图象关于直线
)的图象关于直线 对称,则θ= .
对称,则θ= .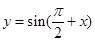 (k∈Z)是奇函数
(k∈Z)是奇函数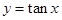 的图象关于点
的图象关于点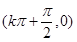 (k∈Z)对称;
(k∈Z)对称;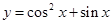 的最小值为
的最小值为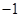 .
.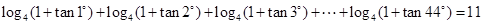
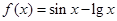 在定义域上有一个零点; 其中正确的是 (填序号).
在定义域上有一个零点; 其中正确的是 (填序号).