题目内容
若数列{an}满足
-
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
}为“调和数列”,且b1+b2+…+b9=90,则b4•b6的最大值是
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| bn |
100
100
.分析:利用新定义,确定{bn}是等差数列,进而可得数列首项与公差的关系,由此可得结论.
解答:解:∵正项数列{
}为“调和数列”,
∴bn+1-bn=d
∴{bn}是等差数列
∵b1+b2+…+b9=90,
∴9b1+
d=90
∴b1+4d=10
∴b1=10-4d
∵b1>0,d≥0
∴0≤d<2.5
∴b4•b6=(10-4d+3d)(10-4d+5d)=100-d2,
∴d=0时,b4•b6的最大值是100
故答案为:100
| 1 |
| bn |
∴bn+1-bn=d
∴{bn}是等差数列
∵b1+b2+…+b9=90,
∴9b1+
| 9×8 |
| 2 |
∴b1+4d=10
∴b1=10-4d
∵b1>0,d≥0
∴0≤d<2.5
∴b4•b6=(10-4d+3d)(10-4d+5d)=100-d2,
∴d=0时,b4•b6的最大值是100
故答案为:100
点评:本题考查新定义,考查等差数列,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
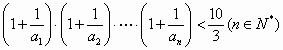
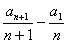 =1,且
=1,且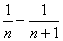 =2(n∈N*),则a10为( )
=2(n∈N*),则a10为( ) =1,且
=1,且 =2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________.
=2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________. =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足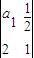 =1,且
=1,且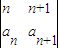 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= . =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足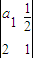 =1,且
=1,且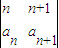 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= .