题目内容
(本题满分15分)已知函数![]() 满足
满足![]() (其中
(其中![]() 为
为![]() 在点
在点![]() 处的导数,
处的导数,![]() 为常数).
为常数).
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)设函数![]() ,若函数
,若函数![]() 在
在![]() 上单调,求实数
上单调,求实数![]() 的取值范围.
的取值范围.
(本题满分15分)
解:(1)由![]() ,得
,得![]() .
.
取![]() ,得
,得![]() ,解之,得
,解之,得![]() , 3分
, 3分
(2)因为![]() .
.
从而![]() ,列表如下:
,列表如下:
|
|
|
|
| 1 |
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 有极大值 | ↘ | 有极小值 | ↗ |
∴![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ;
;
![]() 的单调递减区间是
的单调递减区间是![]() . 8分
. 8分
(3)函数![]() ,
,
有![]() =(–x2– 3 x+C–1)ex , 10分
=(–x2– 3 x+C–1)ex , 10分
当函数在区间![]() 上为单调递增时,等价于h(x)= –x2– 3 x+C–1³0在
上为单调递增时,等价于h(x)= –x2– 3 x+C–1³0在![]() 上恒成立, 只要h(2)³0,解得c ³11, 13分
上恒成立, 只要h(2)³0,解得c ³11, 13分
当函数在区间![]() 上为单调递减时,等价于h(x)= –x2– 3 x+C–1£0在
上为单调递减时,等价于h(x)= –x2– 3 x+C–1£0在![]() 上恒成立, 即
上恒成立, 即![]() =
=![]() ,解得c £ –
,解得c £ –![]() ,
,
所以c的取值范围是c ³11或c £ –![]() . 15分
. 15分

练习册系列答案
相关题目
 (0,1),
(0,1), ,直线
,直线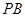 、
、 都是圆
都是圆 的切线(
的切线(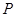 点不在
点不在 轴上).
轴上). 轴上的抛物线的标准方程;
轴上的抛物线的标准方程; 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使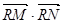 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围. 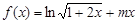 .
.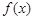 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B, 对称,问是否存在直线
对称,问是否存在直线 ?若存在,求出直线
?若存在,求出直线
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]