题目内容
(本题满分15分)已知圆N: 和抛物线C:
和抛物线C: ,圆的切线
,圆的切线 与抛物线C交于不同的两点A,B,
与抛物线C交于不同的两点A,B,
(1)当直线 的斜率为1时,求线段AB的长;
的斜率为1时,求线段AB的长;
(2)设点M和点N关于直线 对称,问是否存在直线
对称,问是否存在直线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

解:因为圆N: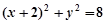 ,
,
所以圆心N为(-2,0),半径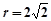 , …………………
1分
, …………………
1分
设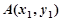 ,
,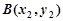 ,
,
(1)当直线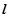 的斜率为1时,设
的斜率为1时,设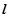 的方程为
的方程为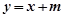 即
即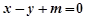
因为直线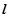 是圆N的切线,所以
是圆N的切线,所以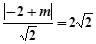 ,解得
,解得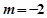 或
或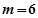 (舍)
(舍)
此时直线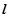 的方程为
的方程为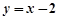 ,
………………… 3分
,
………………… 3分
由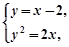 消去
消去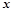 得
得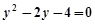 ,
,
所以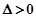 ,
,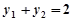 ,
,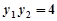 ,
………………… 4分
,
………………… 4分
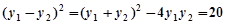
所以弦长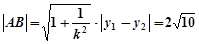 …………………6分
…………………6分
(2)①设直线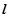 的方程为
的方程为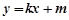 即
即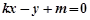 (
(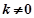 )
)
因为直线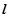 是圆N的切线,所以
是圆N的切线,所以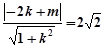 ,
,
得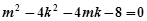 ………① ……………… 8分
………① ……………… 8分
由 消去
消去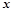 得
得 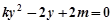 ,
,
所以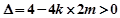 即
即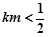 且
且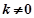 ,
,
 ,
,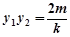 .
………………… 9分
.
………………… 9分
因为点M和点N关于直线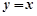 对称,所以点M为
对称,所以点M为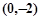
所以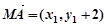 ,
,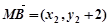 ,
,
因为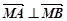 ,所以
,所以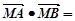
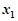
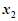 +
+ 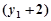
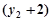
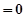 …… 10分
…… 10分
将A,B在直线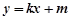 上代入化简得
上代入化简得
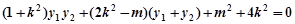 ……… 11分
……… 11分
代入 ,
,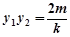 得
得
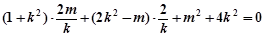
化简得 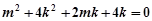 ………②
………… 12分
………②
………… 12分
①+②得 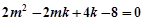
即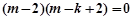 ,解得
,解得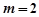 或
或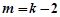
当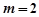 时,代入①解得
时,代入①解得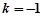 ,满足条件
,满足条件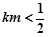 且
且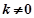 ,
,
此时直线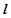 的方程为
的方程为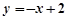 ;
;
当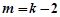 时,代入①整理得
时,代入①整理得 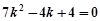 ,无解. …………… 13分
,无解. …………… 13分
② 当直线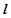 的斜率不存在时,
的斜率不存在时,
因为直线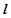 是圆N的切线,所以
是圆N的切线,所以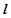 的方程为
的方程为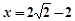 ,
,
则得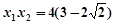 ,
,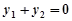 ,
,
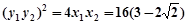 即
即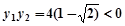
由①得: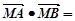
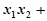
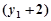
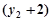
=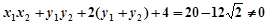
当直线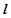 的斜率不存在时
的斜率不存在时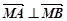 不成立.
……………… 14分
不成立.
……………… 14分
综上所述,存在满足条件的直线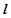 ,其方程为
,其方程为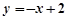 ……………… 15分
……………… 15分
另解:
(2)设直线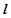 的方程为
的方程为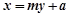 即
即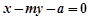 (
(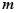 必存在)
必存在)
因为直线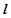 是圆N的切线,所以
是圆N的切线,所以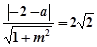 ,
,
得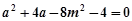 ………① ……………… 8分
………① ……………… 8分
由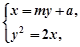 消去
消去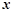 得
得 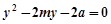 ,
,
所以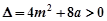 即
即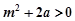 ………………… 9分
………………… 9分
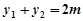 ,
,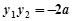 .
………………… 10分
.
………………… 10分
因为点M和点N关于直线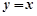 对称,所以点M为
对称,所以点M为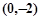
所以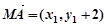 ,
,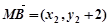 ,
,
因为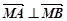 ,所以
,所以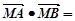
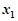
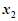 +
+ 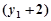
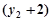
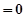 …… 11分
…… 11分
将A,B在直线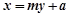 上代入化简得
上代入化简得
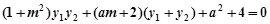 ……… 12分
……… 12分
代入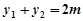 ,
,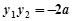 得
得
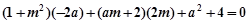
化简得 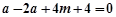 ………②
………… 13分
………②
………… 13分
①+②得 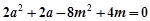
即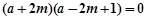 ,解得
,解得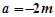 或
或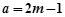 …… 14分
…… 14分
当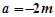 时,代入①解得
时,代入①解得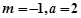 ,满足条件
,满足条件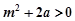 ;
;
当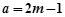 时,代入①整理得
时,代入①整理得 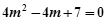 ,无解.
,无解.
综上所述,存在满足条件的直线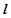 ,其方程为
,其方程为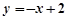 ……………… 15分
……………… 15分
【解析】略

 (0,1),
(0,1), ,直线
,直线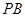 、
、 都是圆
都是圆 的切线(
的切线(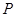 点不在
点不在 轴上).
轴上). 轴上的抛物线的标准方程;
轴上的抛物线的标准方程; 与(Ⅰ)中的抛物线相交于
与(Ⅰ)中的抛物线相交于
 两点,问是否存在定点
两点,问是否存在定点 使
使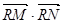 为常数?若存在,求出点
为常数?若存在,求出点 的坐标及常数;若不存在,请说明理由
的坐标及常数;若不存在,请说明理由 ,命题q:
,命题q: . 若“p且q”为真命题,求实数m的取值范围.
. 若“p且q”为真命题,求实数m的取值范围. 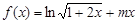 .
.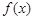 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]