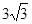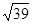题目内容
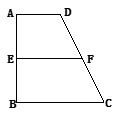
已知梯形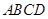 中,
中,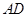 ∥
∥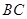 ,
,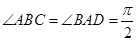 ,
,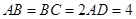 ,
, 、
、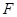 分别是
分别是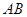 、
、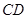 上的点,
上的点,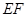 ∥
∥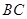 ,
,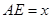 ,
, 是
是 的中点.沿
的中点.沿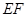 将梯形
将梯形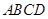 翻折,使平面
翻折,使平面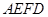 ⊥平面
⊥平面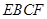 (如图).
(如图).
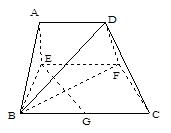
(I)当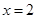 时,求证:
时,求证: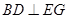 ;
;
(II)若以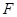 、
、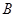 、
、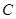 、
、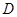 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为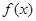 ,求
,求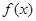 的最大值;
的最大值;
(III)当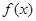 取得最大值时,求二面角
取得最大值时,求二面角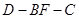 的余弦值.
的余弦值.
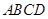 中,
中,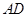 ∥
∥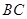 ,
,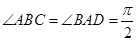 ,
,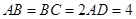 ,
, 、
、 分别是
分别是 、
、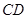 上的点,
上的点,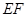 ∥
∥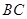 ,
,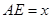 ,
,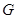 是
是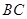 的中点.沿
的中点.沿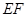 将梯形
将梯形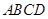 翻折,使平面
翻折,使平面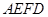 ⊥平面
⊥平面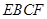 (如图).
(如图).
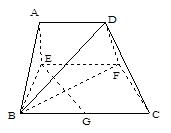
(I)当
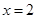 时,求证:
时,求证: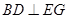 ;
;(II)若以
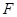 、
、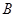 、
、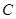 、
、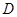 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为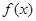 ,求
,求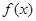 的最大值;
的最大值;(III)当
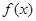 取得最大值时,求二面角
取得最大值时,求二面角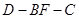 的余弦值.
的余弦值.(1)略
(2)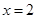 时
时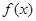 有最大值为
有最大值为 .
.
(3)所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为- .
.
(2)
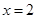 时
时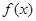 有最大值为
有最大值为 .
. (3)所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-
 .
.(1)作DH⊥EF于H,连BH,GH,
由平面 平面
平面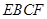 知:DH⊥平面EBCF,而EG
知:DH⊥平面EBCF,而EG 平面EBCF,故EG⊥DH.
平面EBCF,故EG⊥DH.
然后再证明 ,从而可证得
,从而可证得
 .
.
(2) ∵AD∥面BFC, 可把
可把 转化为
转化为 从而可得
从而可得

 ,因而最值可求.
,因而最值可求.
(3)宜采用向量法求解,要先求出二面角二个面的法向量,然后利用法向量的夹角与二面角相等或互补求二面角的大小.
由平面
 平面
平面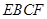 知:DH⊥平面EBCF,而EG
知:DH⊥平面EBCF,而EG 平面EBCF,故EG⊥DH.
平面EBCF,故EG⊥DH.然后再证明
 ,从而可证得
,从而可证得
 .
.(2) ∵AD∥面BFC,
 可把
可把 转化为
转化为 从而可得
从而可得

 ,因而最值可求.
,因而最值可求.(3)宜采用向量法求解,要先求出二面角二个面的法向量,然后利用法向量的夹角与二面角相等或互补求二面角的大小.

练习册系列答案
相关题目
 的中位线
的中位线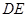 ,将平面
,将平面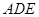 折起,平面
折起,平面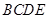 ,得到四棱锥
,得到四棱锥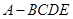 ,
,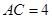 ,设
,设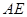 、
、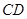 的中点分别为
的中点分别为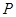 、
、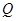 ,
,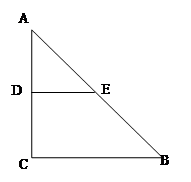
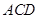



 ,SA=SC=2,,二面角S—AC—B的余弦值是
,SA=SC=2,,二面角S—AC—B的余弦值是 ,若S、A、B、C都在同一球面上,则该球的表面积是
,若S、A、B、C都在同一球面上,则该球的表面积是 B.
B. C.24
C.24 D.6
D.6 内有一个球与正方体的各个面都相切,经过
内有一个球与正方体的各个面都相切,经过 和
和 作一个截面,正确的截面图是 .
作一个截面,正确的截面图是 .




 的主视图、俯视图如下图所示,其中VA=4,AC=
的主视图、俯视图如下图所示,其中VA=4,AC= ,则该三棱锥的左视图的面积;
,则该三棱锥的左视图的面积;