题目内容
已知a=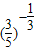 ,b=
,b=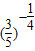 ,c=
,c=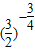 ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( )A.c<a<b
B.a<b<c
C.b<a<c
D.c<b<a
【答案】分析:根据指数函数的单调性可以判断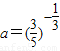 与b=
与b=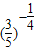 的大小,再判断c=
的大小,再判断c=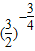 <1,从而进行求解;
<1,从而进行求解;
解答:解:∵a=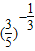 ,b=
,b=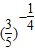 ,
,
∴0< <1,可得y=ax,0<a<1,y是单调减函数,
<1,可得y=ax,0<a<1,y是单调减函数,
- <-
<- ,
,
∴a=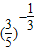 >b=
>b=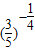 >1,
>1,
∵c=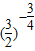 <1,则
<1,则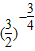 =c<b=
=c<b=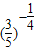 <a=
<a=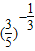 ,
,
∴c<b<a,
故选D;
点评:本题考查大小比较,解题的关键是利用指数函数、对数函数的单调性,确定a,b,c与1的大小关系.
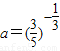 与b=
与b=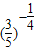 的大小,再判断c=
的大小,再判断c=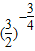 <1,从而进行求解;
<1,从而进行求解;解答:解:∵a=
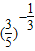 ,b=
,b=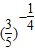 ,
,∴0<
 <1,可得y=ax,0<a<1,y是单调减函数,
<1,可得y=ax,0<a<1,y是单调减函数,-
 <-
<- ,
,∴a=
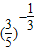 >b=
>b=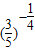 >1,
>1,∵c=
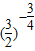 <1,则
<1,则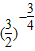 =c<b=
=c<b=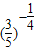 <a=
<a=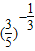 ,
,∴c<b<a,
故选D;
点评:本题考查大小比较,解题的关键是利用指数函数、对数函数的单调性,确定a,b,c与1的大小关系.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角,向量
=(-sinA,1)
=(1,cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |