题目内容
曲线C: 与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
3π
分析:根据新定义,望圆的方程可设为x2+(y-1)2=r2,面积最小的“望圆”的半径为(0,1)到 上任意点之间的最小距离,由此可得结论.
上任意点之间的最小距离,由此可得结论.
解答:根据题意,望圆的方程可设为x2+(y-1)2=r2,面积最小的“望圆”的半径为(0,1)到 上任意点之间的最小距离.
上任意点之间的最小距离.
∵ =(x-1)2+
=(x-1)2+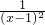 +2(x-1)-
+2(x-1)- +2≥3
+2≥3
∴半径 ,最小面积为3π
,最小面积为3π
故答案为:3π
点评:本题考查新定义,考查直线与圆的位置关系,正确理解新定义,确定圆的半径是关键.
分析:根据新定义,望圆的方程可设为x2+(y-1)2=r2,面积最小的“望圆”的半径为(0,1)到
 上任意点之间的最小距离,由此可得结论.
上任意点之间的最小距离,由此可得结论.解答:根据题意,望圆的方程可设为x2+(y-1)2=r2,面积最小的“望圆”的半径为(0,1)到
 上任意点之间的最小距离.
上任意点之间的最小距离.∵
 =(x-1)2+
=(x-1)2+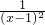 +2(x-1)-
+2(x-1)- +2≥3
+2≥3∴半径
 ,最小面积为3π
,最小面积为3π故答案为:3π
点评:本题考查新定义,考查直线与圆的位置关系,正确理解新定义,确定圆的半径是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 . 与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 . 与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .