题目内容
设向量a=(-1,2),b=(1,-1),c=(3,-2),用a,b作基底可将c表示为c=pa+qb,则实数p,q的值为( ).
| A.p=4,q=1 | B.p=1,q=4 | C.p=0,q=4 | D.p=1,q=-4 |
B
解析试题分析:c=pa+qb,则有 ,解得
,解得 .
.
考点:向量的坐标运算.

练习册系列答案
相关题目
已知 ,
, ,如果
,如果 ∥
∥ ,则实数
,则实数 的值等于 ( )
的值等于 ( )
A. | B. | C. | D. |
平面向量 ,
, ,
, (
( ),且
),且 与
与 的夹角等于
的夹角等于 与
与 的夹角,则
的夹角,则 ( )
( )
A. | B. | C. | D.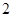 |
如图,在△ 中,
中,  ,
, 是
是 上的一点,若
上的一点,若 ,则实数
,则实数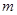 的值为( )
的值为( ) 

A. | B. | C. | D. |
已知向量 与向量
与向量 垂直,则
垂直,则 ( )
( )
A. | B. | C. | D. |
[2014·广州调研]已知向量a=(2,1),b=(x,-2),若a∥b,则a+b等于( )
| A.(-2,-1) | B.(2,1) | C.(3,-1) | D.(-3,1) |
在平行四边形ABCD中,AC为一条对角线,
 =(2,4),
=(2,4), =(1,3),则
=(1,3),则 =( ).
=( ).
| A.(-3,-5) | B.(3,5) | C.(2,4) | D.(-2,-4) |
 +与
+与 在
在 方向上的投影为( )
方向上的投影为( )


