题目内容
如图，在△
中, 
,
是
上的一点,若
,则实数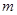
的值为( ) 
A． | B． | C． | D． |
C
解析试题分析：如下图，∵B,P,N三点共线，∴
，∴
，即
,
∴
①,又∵
，∴
，∴
②，
对比①，②，由平面向量基本定理可得：
．
考点：1．平面向量的线性运算；2．平面向量基本定理．
练习册系列答案
相关题目
已知平面向量
=（1，2），
=（﹣2，﹣4），则2+3=（ ）.
| A．（﹣4，﹣8） | B．（﹣5，﹣10） |
| C．（﹣3，﹣6） | D．（﹣2，﹣4） |
表示出来的是（ ）
B .
D.
设向量a＝(－1,2)，b＝(1，－1)，c＝(3，－2)，用a，b作基底可将c表示为c＝pa＋qb，则实数p，q的值为( )．
| A．p＝4，q＝1 | B．p＝1，q＝4 | C．p＝0，q＝4 | D．p＝1，q＝－4 |
设平面向量
，
，若
，则
等于（ ）
A． | B． | C． | D． |
＝
，
＝
，延长AB到D，使BD＝AB，连接CD，则用
＝ ．
（2012•广东）若向量
，向量
，则
=（ ）
| A．（﹣2，﹣4） | B．（3，4） | C．（6，10） | D．（﹣6，﹣10） |
已知点A(1，3)，B(4，－1)，则与向量
同方向的单位向量为( )
A．( ，－ ) |
| B．(，－) |
| C．(－，) |
| D．(－，) |
已知向量a＝(－1，1)，b＝(3，m)，a∥(a＋b)，则m＝( )
| A．2 | B．－2 | C．－3 | D．3 |