题目内容

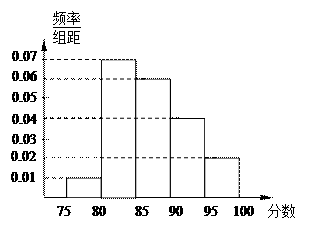
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分)，其中120分(含120分)以上为优秀，绘制了如下的两个频率分布直方图：

男生

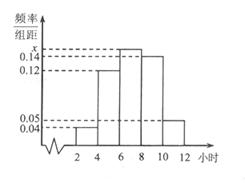
女生
(1)根据以上两个直方图完成下面的2×2列联表：

成绩性别
优秀
不优秀
总计
男生
 
 
 
女生
 
 
 
总计
 
 
 
 
(2)根据(1)中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？
(注：
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
 
K2＝，其中n＝a＋b＋c＋d.)
(3)若从成绩在[130,140]的学生中任取2人，求取到的2人中至少有1名女生的概率．

（1）

成绩性别
优秀
不优秀
总计
男生
13
10
23
女生
7
20
27
总计
20
30
50
 
（2）有95%的把握认为学生的数学成绩与性别之间有关系
（3）

解析

练习册系列答案
相关题目

某小学四年级男同学有45名，女同学有30名，老师按照分层抽样的方法组建了一个5人的课外兴趣小组.
（Ⅰ）求某同学被抽到的概率及课外兴趣小组中男、女同学的人数；
（Ⅱ）经过一个月的学习、讨论，这个兴趣小组决定选出两名同学做某项实验，方法是先从小组里选出1名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率.

为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下

 
男
女
合计
需要
40
30
 
不需要
160
270
 
合计
 
 
 
（1）将表格填写完整，并估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
（2）能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关系?
（3）根据（2）的结论,能否提出更好的调查方法估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附表：
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
 

（本小题满分10分）某班主任对班级22名学生进行了作业量多少的调查，数据如下表：在喜欢玩电脑游戏的12中，有10人认为作业多，2人认为作业不多；在不喜欢玩电脑游戏的10人中，有3人认为作业多，7人认为作业不多.求：
（1）根据以上数据建立一个列联表；
（2）试问喜欢电脑游戏与认为作业多少是否有关系？

某地最近十年粮食需求量逐年上升，下表是部分统计数据：

年份
2004
2006
2008
2010
2012
需求量(万吨)
236
246
257
276
286
 
(1)利用所给数据求年需求量与年份之间的回归直线方程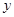＝x＋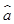
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量．

随着工业化以及城市车辆的增加，城市的空气污染越来越严重，空气质量指数API一直居高不下，对人体的呼吸系统造成了严重的影响．现调查了某市500名居民的工作场所和呼吸系统健康，得到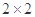列联表如下：

 
室外工作
室内工作
合计
有呼吸系统疾病
150
 
 
无呼吸系统疾病
 
100
 
合计
200
 
 
 
（1）补全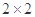列联表；
（2）你是否有95%的把握认为感染呼吸系统疾病与工作场所有关；

某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：


2
3
4
5
6

2.2
3.8
5.5
6.5
7.0
 
已知，，
(1)在下面坐标系中画出散点图；

(2)计算，，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?

某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组
[95，100]得到的频率分布直方图如图所示．
(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率．

某校为了解高三同学寒假期间学习情况，抽查了100名学生，统计他们每天平均学习时间，绘成频率分布直方图（如图）。则这100名同学中学习时间6~8小时的人数为         。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网