题目内容
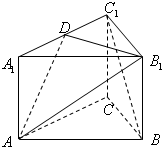 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
| ||
| 2 |
(1)若A1D=DC1,求证:直线BC1∥平面AB1D;
(2)是否存点D,使平面AB1D⊥平面ABB1A1,若存在,请确定点D的位置,若不存在,请说明理由;
(3)请指出点D的位置,使二面角A1-AB1-D平面角的正切值的大小为2,并证明你的结论.
分析:(1)连接A1B交AB1于E点,由A1D=DC1,结合三角形中位线定理可得DE∥BC1,进而根据线面平行的判定定理得到直线BC1∥平面AB1D;
(2)过点D作DN⊥AB1于N,过D作DM⊥A1B1于M,由线面垂直的判定定理及同一法,可得M、N应重合于B1点,由点D在棱A1C1上,故∠A1B1D≤∠A1B1C1=600,故不存在这样的点D,使平面AB1D⊥平面ABB1A1.
(3)连接MN,过A1作A1F⊥AB1于F.由(2)的结合可得∠MND为二面角A1-AB1-D平面角,设
=λ,由二面角A1-AB1-D平面角的正切值的大小为2,我们易构造关于λ的方程,解方程求出λ的值,即可指出点D的位置.
(2)过点D作DN⊥AB1于N,过D作DM⊥A1B1于M,由线面垂直的判定定理及同一法,可得M、N应重合于B1点,由点D在棱A1C1上,故∠A1B1D≤∠A1B1C1=600,故不存在这样的点D,使平面AB1D⊥平面ABB1A1.
(3)连接MN,过A1作A1F⊥AB1于F.由(2)的结合可得∠MND为二面角A1-AB1-D平面角,设
| A1D |
| A1C1 |
解答:解: (1)证明:连接A1B交AB1于E点,
(1)证明:连接A1B交AB1于E点,
在平行四边形ABB1A1中,有A1E=BE,又A1D=DC1…(2分)
∴DE为△A1BC1的中位线,从而DE∥BC1,
又DE?平面AB1D,BC1?平面AB1D,
∴直线BC1∥平面AB1D…(4分)
(2)假设存在点D,使平面AB1D⊥平面ABB1A1,
过点D作DN⊥AB1于N,则DN⊥平面ABB1A1,
又过D作DM⊥A1B1于M,则DM⊥平面ABB1A1,…(6分)
而过平面外一点有且仅有一条直线与已知平面垂直,故M、N应重合于B1点,此时应有DB1⊥A1B1,故∠A1B1D=90°,…(7分)
又点D在棱A1C1上,故∠A1B1D≤∠A1B1C1=600,
显然矛盾,故不存在这样的点D,使平面AB1D⊥平面ABB1A1.…(9分)
(3)连接MN,过A1作A1F⊥AB1于F.
由(2)中的作法可知:∠MND为二面角A1-AB1-D平面角,…(10分)
设
=λ,则
=
,
则可得DM=
λ,A1F=
a,
=1-
⇒MN=
(1-
),…(12分)
∴tanθ=
=
=-3+
.∴-3+
=2⇒λ=
即点D在棱A1C1上,且
=
时,
二面角A1-AB1-D平面角的正切值的大小为2. …(14分)
 (1)证明:连接A1B交AB1于E点,
(1)证明:连接A1B交AB1于E点,在平行四边形ABB1A1中,有A1E=BE,又A1D=DC1…(2分)
∴DE为△A1BC1的中位线,从而DE∥BC1,
又DE?平面AB1D,BC1?平面AB1D,
∴直线BC1∥平面AB1D…(4分)
(2)假设存在点D,使平面AB1D⊥平面ABB1A1,
过点D作DN⊥AB1于N,则DN⊥平面ABB1A1,
又过D作DM⊥A1B1于M,则DM⊥平面ABB1A1,…(6分)
而过平面外一点有且仅有一条直线与已知平面垂直,故M、N应重合于B1点,此时应有DB1⊥A1B1,故∠A1B1D=90°,…(7分)
又点D在棱A1C1上,故∠A1B1D≤∠A1B1C1=600,
显然矛盾,故不存在这样的点D,使平面AB1D⊥平面ABB1A1.…(9分)
(3)连接MN,过A1作A1F⊥AB1于F.
由(2)中的作法可知:∠MND为二面角A1-AB1-D平面角,…(10分)
设
| A1D |
| A1C1 |
| A1M |
| A1B1 |
| λ |
| 2 |
则可得DM=
| ||
| 2 |
| ||
| 3 |
| MN |
| A1F |
| λ |
| 2 |
| ||
| 3 |
| λ |
| 2 |
∴tanθ=
| DM |
| MN |
| ||||||
|
| 6 |
| 2-λ |
| 6 |
| 2-λ |
| 4 |
| 5 |
即点D在棱A1C1上,且
| A1D |
| A1C1 |
| 4 |
| 5 |
二面角A1-AB1-D平面角的正切值的大小为2. …(14分)
点评:本题考查的知识点是与二面角有关的立体几何综合体,直线与平面平行的判定,平面与平面垂直的判定,其中(1)的关键是证得DE∥BC1,(2)的关键是使用反证法和同一法等间接手法进行证明,(3)的关键是根据已知条件构造关于λ的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )
如图,正三棱柱ABC-A1B1C1的各棱长都2,E,F分别是AB,A1C1的中点,则EF的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、
|
 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.