题目内容
15、设直角三角形的两直角边的长分别为a,b,斜边长为c,斜边上的高为h,则有a+b<c+h成立,某同学通过类比得到如下四个结论:①a2+b2>c2+h2;②a3+b3<c3+h3;③a4+b4>c4+h4;④a5+b5<c5+h5.
其中正确结论的序号是
其中正确结论的序号是
②④
;进一步类比得到的一般结论是an+bn<cn+hn(n∈N*)
.分析:由a+b<c+h成立,我们可以类比给出a3+b3<c3+h3;a4+b4<c4+h4;a5+b5<c5+h5等,再逐一分析它们的真假,再根据其中的规律,归纳猜想出一般性的结论.
解答:解:在直角三角形ABC中,a=csinA,b=ccosA,ab=ch,所以h=csinAcosA.
于是an+bn=cn(sinnA+cosnA),cn+hn=cn(1+sinnAcosnA).an+bn-cn-hn=cn(sinnA+cosnA-1-sinnAcosnA)=cn(sinnA-1)(1-cosnA)<0.
所以an+bn<cn+hn(n∈N*).
于是an+bn=cn(sinnA+cosnA),cn+hn=cn(1+sinnAcosnA).an+bn-cn-hn=cn(sinnA+cosnA-1-sinnAcosnA)=cn(sinnA-1)(1-cosnA)<0.
所以an+bn<cn+hn(n∈N*).
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想)

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 ,
, ,则它绕
,则它绕 旋转一周得到的旋转体的体积为 .
旋转一周得到的旋转体的体积为 .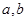 ,斜边长为
,斜边长为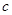 ,斜边上的高为
,斜边上的高为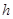 ,则有
,则有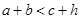 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: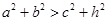 ;②
;②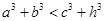 ;③
;③ 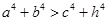 ;④
;④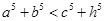 .
.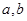 ,斜边长为
,斜边长为 ,斜边上的高为
,斜边上的高为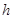 ,则有
,则有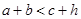 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: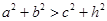 ;②
;②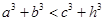 ;③
;③ 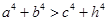 ;④
;④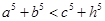 .
.