题目内容
设直角三角形的两直角边AB=3,AC=4,则它绕AB旋转一周得到的旋转体的体积为 .
分析:根据题意可知:所得的立体图形是一个圆锥,AB的长度即圆锥的高,另一条直角边是圆锥的底面半径;然后根据“圆锥的体积=
πr2h”,代入数值,解答即可.
| 1 |
| 3 |
解答:解:根据题意可知所得的立体图形是一个圆锥:底面半径是4,高为3,
圆锥的体积:π×42×3×
,
=π×16×1,
=16π;
故答案为:16π.
圆锥的体积:π×42×3×
| 1 |
| 3 |
=π×16×1,
=16π;
故答案为:16π.
点评:本题考查旋转体的体积的求法,解答此题的关键是:能够想象出所得的立体图形的形状和特征,能灵活运用圆锥的体积计算公式进行解答.

练习册系列答案
相关题目
 ,
, ,则它绕
,则它绕 旋转一周得到的旋转体的体积为 .
旋转一周得到的旋转体的体积为 .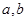 ,斜边长为
,斜边长为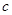 ,斜边上的高为
,斜边上的高为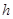 ,则有
,则有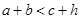 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: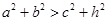 ;②
;②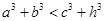 ;③
;③ 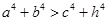 ;④
;④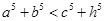 .
.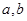 ,斜边长为
,斜边长为 ,斜边上的高为
,斜边上的高为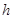 ,则有
,则有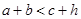 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论: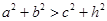 ;②
;②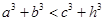 ;③
;③ 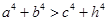 ;④
;④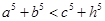 .
.