��Ŀ����
5����ֱ������ϵ�У���OΪ���㣬x���������Ϊ���ᣬ��������ϵȡ��ͬ�ij��ȵ�λ����֪ԲC�ļ����귽���Ǧ�=2$\sqrt{2}$cos����+$\frac{��}{4}$������ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=t}\\{y=-1+2\sqrt{2t}}\end{array}\right.$��tΪ��������ֱ��l��ԲC����A��B���㣬P��ԲC�ϲ�ͬ��A��B������һ�㣬��1����ԲC��Բ�ĵļ����ꣻ
��2����������PAB��������ֵ��
���� ��1������y=��sin�ȣ�x=��cos�ȣ���C�ļ����귽�̻���ֱ�����귽�̣��ɵ�ԲC��Բ�ĵļ����ꣻ
��2�����P��ֱ��AB��������ֵ��|AB|��������������PAB��������ֵ��
��� �⣺��1��ԲC�ļ����귽���Ǧ�=2$\sqrt{2}$cos����+$\frac{��}{4}$������Ϊ��=2cos��-2sin�ȣ�
���2=2��cos��-2��sin�ȣ�
�ɦ�cos��=x����sin��=y����x2+y2-2x+2y=0������x-1��2+��y+1��2=2��
��Բ������Ϊ��1��-1����������Ϊ��$\sqrt{2}$��$\frac{7��}{4}$����
��2��ֱ�ߵ���ͨ����Ϊ2$\sqrt{2}$x-y-1=0��
Բ�ĵ�ֱ��l�ľ���Ϊd=$\frac{|2\sqrt{2}+1-1|}{3}$=$\frac{2\sqrt{2}}{3}$��
���ҳ�|AB|=2$\sqrt{2-\frac{8}{9}}$=$\frac{2\sqrt{10}}{3}$��
��P��ֱ��AB��������ֵΪ$\sqrt{2}$+$\frac{2\sqrt{2}}{3}$=$\frac{5\sqrt{2}}{3}$��
��������PAB��������ֵΪ$\frac{1}{2}��\frac{2\sqrt{10}}{3}��\frac{5\sqrt{2}}{3}=\frac{10\sqrt{5}}{9}$��
���� �������е��⣬���鼫���귽����ֱ�����귽�̵Ļ������㵽ֱ�ߵľ��빫ʽ��Ӧ�ã��������������

| A�� | $\sqrt{3}$ | B�� | 1 | C�� | 4 | D�� | 3 |
| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{8}$ |
 �������� ��
�������� ��
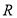 ���
�ĺ��� ���溯��.
���溯��. ��ֵ��
��ֵ��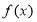 ��
��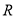 ���ǵ����ݼ�������
���ǵ����ݼ������� ������ʽ
������ʽ ���������
��������� ��ȡֵ��Χ.
��ȡֵ��Χ.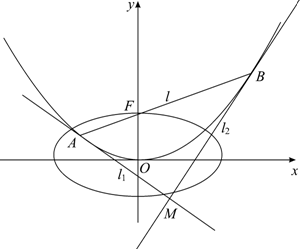 ��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$��
��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$��