题目内容
15.已知集合A={x|3≤3x≤27},B={x|x>2},全集U=R.(1)求(∁UB)∪A;
(2)已知集合C={x|1<x<a},若C⊆A,求实数a的取值范围.
分析 (1)化简A=[1,3],B={x|x>2}=(2,+∞),从而求得;
(2)分类讨论,从而确定a的取值范围.
解答 解:(1)A={x|3≤3x≤27}=[1,3],B={x|x>2}=(2,+∞),
故(∁UB)∪A=(-∞,2]∪[1,3]=(-∞,3];
(2)①当a≤1时,C=∅,此时C⊆A;
②当a>1时,C⊆A,则1<a≤3;
综合①②,可得a的取值范围是(-∞,3].
点评 本题考查了集合的化简与运算,同时考查了分类讨论的思想应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
6.若三角形三边长之比是1:$\sqrt{3}$:2,则其所对角之比是( )
| A. | 1:2:3 | B. | 1:$\sqrt{3}$:2 | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{2}$:$\sqrt{3}$:2 |
4.某商店经营一批进价为每千克3.5元的商品,调查发现,此商品的销售单价x(元/千克)与日销量y(千克)之间有如下关系:
若x与y具有线性相关关系y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,且$\stackrel{∧}{b}$=-2.6为使日销售利润最大,则销售单价应定为(结果保留一位小数)( )
| x | 5 | 6 | 7 | 8 |
| y | 20 | 17 | 15 | 12 |
| A. | 7.5 | B. | 7.8 | C. | 8.1 | D. | 8.4 |
5.sin14°cos74°-cos14°sin74°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
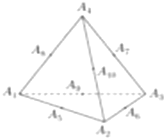 已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.
已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.