Question

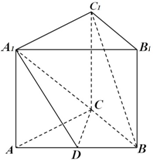（2012•长春模拟）已知直三棱柱ABC-A₁B₁C₁中，AC⊥CB，D为AB中点，A₁A=AC=

3

，CB=1．
（1）求证：BC₁∥平面A₁CD；
（2）求三棱锥C₁-A₁DC的体积．

Answer 1

分析：（1）要证BC₁∥平面A₁CD，只需证明BC₁∥平面A₁CD内的一条直线即可，由于已知的三条直线A₁C，A₁D，DC，都不与BC₁平行，故需添加辅助线完成；
（2）要求三棱锥的体积，关键找到合适的底面和高，而在此我们可以用等体积来转化．

解答：解：（1）证明：连接AC₁∩A₁C=O，连接DO，则O和D分别为AC₁和AB的中点，
∴DO∥BC₁，而DO?面A₁DC，BC₁?面A₁DC，
∴BC₁∥面A₁DC．
（2）∵BC₁∥面A₁DC，∴C₁和B到平面A₁DC的距离相等，
从而有V三棱锥C1-A1DC=V三棱锥A1-BDC
=

1

3

S△BDC•AA1=

1

3

×

1

2

S△ABC•AA1，
=

1

6

×

1

2

AC•BC•AA1=

1

6

×

1

2

×

3

×1×

3

=

1

4

．

点评：本小题主要考查立体几何的相关知识，具体涉及到线面的平行关系、几何体的体积的求法等知识．