题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
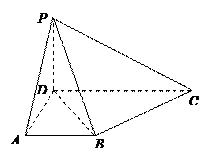
在四棱锥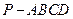 中,侧面
中,侧面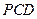
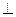 底面
底面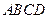 ,
,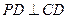 ,底面
,底面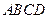 是直角梯形,
是直角梯形,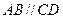 ,
,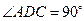 ,
,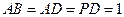 ,
,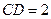 .
.
(Ⅰ)求证: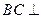 平面
平面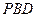 ;
;
(Ⅱ)设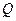 为侧棱
为侧棱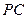 上一点,
上一点,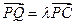 ,
,
试确定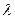 的值,使得二面角
的值,使得二面角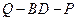 为
为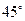 .
.
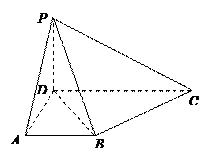
在四棱锥
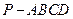 中,侧面
中,侧面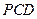
 底面
底面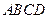 ,
,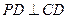 ,底面
,底面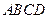 是直角梯形,
是直角梯形,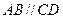 ,
,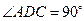 ,
,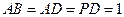 ,
,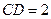 .
.(Ⅰ)求证:
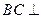 平面
平面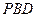 ;
;(Ⅱ)设
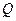 为侧棱
为侧棱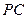 上一点,
上一点,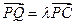 ,
,试确定
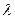 的值,使得二面角
的值,使得二面角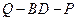 为
为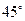 .
.解法一:
(Ⅰ)平面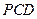
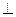 底面
底面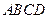 ,
,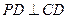 ,所以
,所以 平面
平面 ,………1分
,………1分
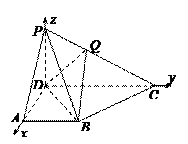 所以
所以 , .……2分
, .……2分
如图,以 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.
则 ………3分
………3分
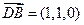 ,
, ,
,
所以 ,
, ,……………4分
,……………4分
又由 平面
平面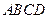 ,可得
,可得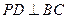 ,所以
,所以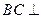 平面
平面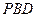 .……………6分
.……………6分
(Ⅱ)平面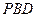 的法向量为
的法向量为 ,…………………………………………7分
,…………………………………………7分
 ,
,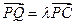 ,
,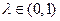
所以 , ………………………………………………………………8分
, ………………………………………………………………8分
设平面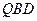 的法向量为
的法向量为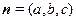 ,
,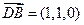 ,
,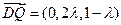 ,
,
由 ,
,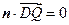 ,得
,得
所以, ,………………………………………………….……9分
,………………………………………………….……9分
所以 ,………………………………………………………….…10分
,………………………………………………………….…10分
所以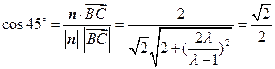 ,……………………...……11分
,……………………...……11分
注意到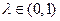 ,得
,得 . …………………………….………………12分
. …………………………….………………12分
法二:(Ⅰ)∵面PCD⊥底面ABCD,面PCD∩底面ABCD=CD,PD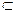 面PCD,且PD⊥CD
面PCD,且PD⊥CD
∴PD⊥面ABCD,………1分 又BC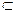 面ABCD,∴BC⊥PD ①…. .…..……2分
面ABCD,∴BC⊥PD ①…. .…..……2分
取CD中点E,连结BE,则BE⊥CD,且BE=1
在Rt△ABD中,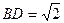 ,在Rt△BCE中,BC=
,在Rt△BCE中,BC=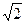 . .……………………...……4分
. .……………………...……4分
∵ , ∴BC⊥BD ②………………...……5分
, ∴BC⊥BD ②………………...……5分
由①、②且PD∩BD=D
∴BC⊥面PBD. ……….………………………………………….…...……6分
(Ⅱ)过Q作QF//BC交PB于F,过F作FG⊥BD于G,连结 GQ.
∵BC⊥面PBD,QF//BC
∴QF⊥面PBD,∴FG为QG在面PBD上的射影,
又∵BD⊥FG ∴BD⊥QG
∴∠FGQ为二面角Q-BD-P的平面角;由题意,∠FGQ="45°." …………….…...……8分
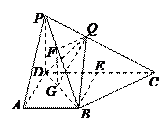 设PQ=x,易知
设PQ=x,易知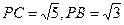
∵FQ//BC,∴
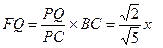
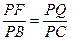
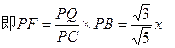
∵FG//PD∴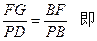
 ………………..…...……10分
………………..…...……10分
在Rt△FGQ中,∠FGQ=45°
∴FQ=FG,即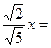
 ∴
∴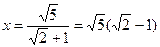 ……..….........……11分
……..….........……11分
∵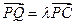 ∴
∴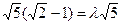 ∴
∴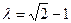 ……..…............……12分
……..…............……12分
(Ⅰ)平面
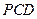
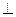 底面
底面 ,
,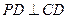 ,所以
,所以 平面
平面 ,………1分
,………1分 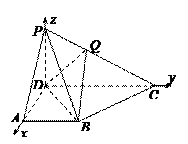 所以
所以 , .……2分
, .……2分如图,以
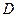 为原点建立空间直角坐标系
为原点建立空间直角坐标系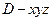 .
.则
 ………3分
………3分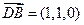 ,
, ,
,所以
 ,
, ,……………4分
,……………4分又由
 平面
平面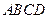 ,可得
,可得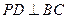 ,所以
,所以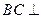 平面
平面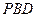 .……………6分
.……………6分(Ⅱ)平面
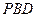 的法向量为
的法向量为 ,…………………………………………7分
,…………………………………………7分 ,
,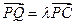 ,
,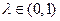
所以
 , ………………………………………………………………8分
, ………………………………………………………………8分设平面
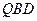 的法向量为
的法向量为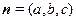 ,
,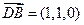 ,
,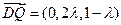 ,
,由
 ,
,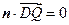 ,得
,得所以,
 ,………………………………………………….……9分
,………………………………………………….……9分所以
 ,………………………………………………………….…10分
,………………………………………………………….…10分所以
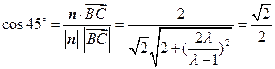 ,……………………...……11分
,……………………...……11分注意到
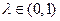 ,得
,得 . …………………………….………………12分
. …………………………….………………12分 法二:(Ⅰ)∵面PCD⊥底面ABCD,面PCD∩底面ABCD=CD,PD
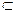 面PCD,且PD⊥CD
面PCD,且PD⊥CD∴PD⊥面ABCD,………1分 又BC
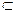 面ABCD,∴BC⊥PD ①…. .…..……2分
面ABCD,∴BC⊥PD ①…. .…..……2分取CD中点E,连结BE,则BE⊥CD,且BE=1
在Rt△ABD中,
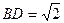 ,在Rt△BCE中,BC=
,在Rt△BCE中,BC=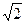 . .……………………...……4分
. .……………………...……4分∵
 , ∴BC⊥BD ②………………...……5分
, ∴BC⊥BD ②………………...……5分由①、②且PD∩BD=D
∴BC⊥面PBD. ……….………………………………………….…...……6分
(Ⅱ)过Q作QF//BC交PB于F,过F作FG⊥BD于G,连结 GQ.
∵BC⊥面PBD,QF//BC
∴QF⊥面PBD,∴FG为QG在面PBD上的射影,
又∵BD⊥FG ∴BD⊥QG
∴∠FGQ为二面角Q-BD-P的平面角;由题意,∠FGQ="45°." …………….…...……8分
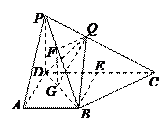 设PQ=x,易知
设PQ=x,易知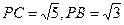
∵FQ//BC,∴

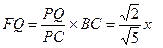
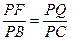
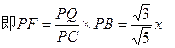
∵FG//PD∴
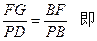
 ………………..…...……10分
………………..…...……10分在Rt△FGQ中,∠FGQ=45°
∴FQ=FG,即
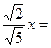
 ∴
∴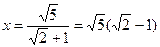 ……..….........……11分
……..….........……11分∵
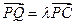 ∴
∴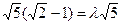 ∴
∴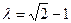 ……..…............……12分
……..…............……12分略

练习册系列答案
相关题目
 ,AA1=4,点D是AB的中点。
,AA1=4,点D是AB的中点。 的体积。
的体积。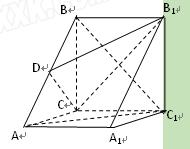

 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
 ,
,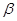 ,
,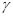 两两互相垂直,点
两两互相垂直,点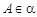 ,点
,点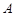 到
到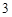 ,点
,点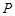 是
是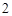 倍,则点
倍,则点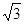
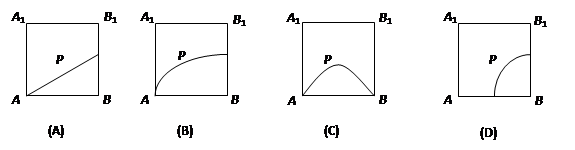
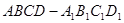 的侧面
的侧面 内有一动点
内有一动点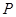 到直线
到直线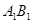 与直线
与直线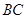 的距离相等,则动点
的距离相等,则动点