题目内容
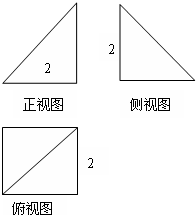（2012•许昌三模）一个几何体的三视图如图所示，则该几何体的外接球体积为4
π
| 3 |
4
π
．| 3 |
分析：由三视图得到这是一个四棱锥，底面是一个边长是2的正方形，一条侧棱与底面垂直，根据四棱锥的对称性知，外接球的直径是AC，利用勾股定理做出球的直径，得到球的体积．
解答：
解：由主视图和左视图是腰长为2的两个全等的等腰直角三角形，
得到这是一个四棱锥，
底面是一个边长是2的正方形，一条侧棱AE与底面垂直，
∴根据四棱锥的对称性知，外接球的直径是AC
根据直角三角形的勾股定理知AC=
=2
，
∴外接球的 体积是
×π×（
）3=4
π，
故答案为：4
π．
解：由主视图和左视图是腰长为2的两个全等的等腰直角三角形，得到这是一个四棱锥，
底面是一个边长是2的正方形，一条侧棱AE与底面垂直，
∴根据四棱锥的对称性知，外接球的直径是AC
根据直角三角形的勾股定理知AC=
| 22+22+22 |
| 3 |
∴外接球的 体积是
| 4 |
| 3 |
| 3 |
| 3 |
故答案为：4
| 3 |
点评：本题考查由三视图求几何体的面积，考查球的体积．考查多面体的外接球的运算，这是一个综合题目，解题时注意几何体对称性的应用．
练习册系列答案
相关题目
（2012•许昌三模）如图，在RT△ABC中，D是斜边AB上一点，且AC=AD，记∠BCD=β，∠ABC=α．
（2012•许昌三模）如图，在四面体ABCD中，二面角A-CD-B的平面角为60°，AC⊥CD，BD⊥CD，且AC=CD=2BD，点E、F分别是AD、BC的中点．