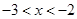题目内容
已知不等式 的解集是[2,3),求不等式
的解集是[2,3),求不等式 -(mx-b)≥0的解.
-(mx-b)≥0的解.
解:由已知不等式 的解集是[2,3),可得 a=2,b=3.
的解集是[2,3),可得 a=2,b=3.
原不等式可化为 ≥0,即
≥0,即  ≤0,化简可得
≤0,化简可得  .
.
当m=1时,不等式的解集是{x|x<2}.
当m>0,且 m≠1时,不等式的解集是 {x|x≤ }.
}.
当m=0时不等式的解是R.
当m<0时不等式的解集是 {x|x≥ }.
}.
分析:由已知解得 a=2,b=3;原不等式可化为 ,分m=1、m>0 且 m≠1、m=0、m<0四种情况,分别求出不等式的解集.
,分m=1、m>0 且 m≠1、m=0、m<0四种情况,分别求出不等式的解集.
点评:本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于中档题.
 的解集是[2,3),可得 a=2,b=3.
的解集是[2,3),可得 a=2,b=3.原不等式可化为
 ≥0,即
≥0,即  ≤0,化简可得
≤0,化简可得  .
.当m=1时,不等式的解集是{x|x<2}.
当m>0,且 m≠1时,不等式的解集是 {x|x≤
 }.
}.当m=0时不等式的解是R.
当m<0时不等式的解集是 {x|x≥
 }.
}.分析:由已知解得 a=2,b=3;原不等式可化为
 ,分m=1、m>0 且 m≠1、m=0、m<0四种情况,分别求出不等式的解集.
,分m=1、m>0 且 m≠1、m=0、m<0四种情况,分别求出不等式的解集.点评:本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
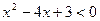 的解集是
的解集是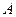 .
.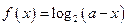
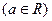 的定义域为集合
的定义域为集合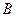 ,若
,若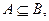
 求
求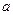 的取值范围;
的取值范围;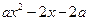

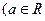 且
且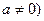 的解集为
的解集为 ,若
,若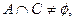 求
求 值范围.
值范围.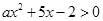 的解集是
的解集是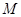 .
.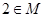 ,求
,求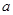 的取值范围;
的取值范围; ,求不等式
,求不等式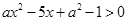 的解集.
的解集. 的解集是
的解集是 ,则
,则  B、
B、
 D、
D、
 的解集是
的解集是 ,则不等式
,则不等式 的解是( )
的解是( )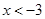 或
或 B、
B、 或
或
 D、
D、
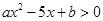 的解集是
的解集是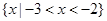 ,则不等式
,则不等式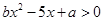 的
的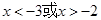 B.
B.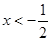 或
或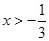 C.
C. D.
D.