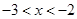题目内容
已知不等式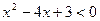 的解集是
的解集是 .
.
(Ⅰ)求集合 ;
;
(Ⅱ)函数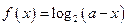
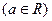 的定义域为集合
的定义域为集合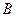 ,若
,若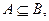
 求
求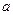 的取值范围;
的取值范围;
(Ⅲ)不等式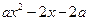

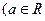 且
且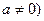 的解集为
的解集为 ,若
,若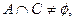 求
求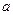 的取
的取 值范围.
值范围.
解:
(Ⅰ) ……4分
……4分
(Ⅱ) ; ……8分
; ……8分
(Ⅲ)设
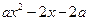
 时,
时, ;
; 时,
时,
则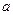 的取值范围是
的取值范围是
……15分
另解:∵ 为二次函数,∴
为二次函数,∴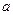 ≠0,令
≠0,令 =0,
=0,
解得其两根为 =
= -
- <0,
<0, =
= +
+ >0
>0
①当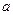 >0时,
>0时,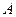 ={
={ |
| <
< 或
或 >
> },又知集合
},又知集合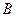 ={
={ |1<
|1< <3},
<3}, ≠
≠ ,
,
则满足: <3,即
<3,即 +
+ <3,∴
<3,∴
②当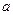 <0时,
<0时,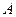 ={
={ |
| <
< <
< },
}, ≠
≠ 其满足
其满足 >1,即
>1,即 +
+ >1,解得
>1,解得
综上所述,使 ≠
≠ 成立的
成立的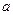 的取值范围是
的取值范围是
解析

练习册系列答案
相关题目
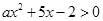 的解集是
的解集是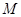 .
.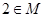 ,求
,求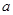 的取值范围;
的取值范围; ,求不等式
,求不等式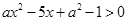 的解集.
的解集. 的解集是
的解集是 ,则
,则  B、
B、
 D、
D、
 的解集是
的解集是 ,则不等式
,则不等式 的解是( )
的解是( )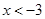 或
或 B、
B、 或
或
 D、
D、
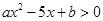 的解集是
的解集是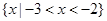 ,则不等式
,则不等式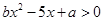 的
的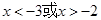 B.
B.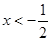 或
或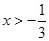 C.
C.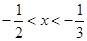 D.
D.