题目内容
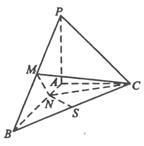
 已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=0.5 AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=0.5 AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
证明:
设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。

则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,![]() ),N(
),N(![]() ,0,0),S(1,
,0,0),S(1,![]() ,0).……4分
,0).……4分
(Ⅰ)![]() ,
,
因为![]() ,
,
所以CM⊥SN ……6分
(Ⅱ)![]() ,
,
设a=(x,y,z)为平面CMN的一个法向量,
则 ……9分
……9分
因为
所以SN与片面CMN所成角为45°。 ……12分

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
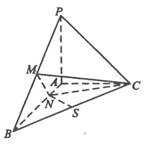
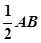 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.