题目内容
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.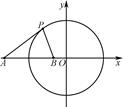
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有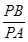 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
(1)y=-2x±3 (2)
(2)
解析

练习册系列答案
相关题目
设椭圆C1和抛物线C2的焦点均在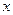 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
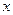 | 3 | -2 | 4 | 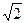 |
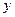 | 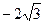 | 0 | -4 | 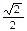 |
(1)求曲线C1,C2的标准方程;
(2)设直线
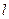 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且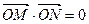 。请问是否存在直线
。请问是否存在直线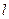 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线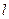 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.  中,顶点
中,顶点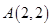 ,边
,边 上的中线
上的中线 所在直线的方程是
所在直线的方程是 ,边
,边 上高
上高 所在直线的方程是
所在直线的方程是 .
. 、C的坐标; (2)求
、C的坐标; (2)求 过点P(2,1),夹在两已知直线
过点P(2,1),夹在两已知直线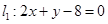 和
和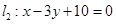 之间的线段AB恰被点P平分.
之间的线段AB恰被点P平分.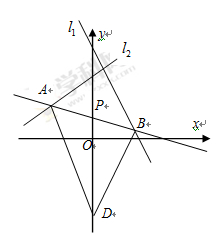
 的方程;
的方程; ,求:
,求: ABD的面积.
ABD的面积. ,直线
,直线 与
与 关于直线
关于直线 对称,则直线
对称,则直线