题目内容
5.如图,已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,P、Q在渐近线上,PQ的中垂线过点F,O是坐标原点,若∠PFQ=Rt∠,OQ=3OP,则双曲线的离心率等于( )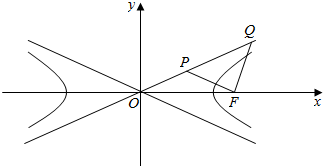
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
分析 取PQ的中点A,连接AF,则AF⊥PQ,确定OA=2AF,由勾股定理可得AF=$\frac{1}{\sqrt{5}}$c,利用AF=$\frac{bc}{\sqrt{{b}^{2}+{a}^{2}}}$=b,即可得出结论.
解答 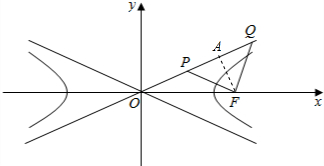 解:取PQ的中点A,连接AF,则AF⊥PQ,
解:取PQ的中点A,连接AF,则AF⊥PQ,
∵∠PFQ=Rt∠,OQ=3OP,
∴OA=2AF,
由勾股定理可得AF2+OA2=c2,
∴AF=$\frac{1}{\sqrt{5}}$c,
∵AF=$\frac{bc}{\sqrt{{b}^{2}+{a}^{2}}}$=b,
∴b=$\frac{1}{\sqrt{5}}$c,
∴a=$\frac{2}{\sqrt{5}}$c,
∴$e=\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查双曲线的性质,考查勾股定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
16.在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c满足b2=a2+c2-ac,若AC=2$\sqrt{3}$,则△ABC面积的最大值为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |