题目内容
10．设数列{an}的前n项为Sn，且满足2Sn-nan=10n．证明数列{an}是等差数列．分析 当n=1时，求得a1=10，再将n换成n-1，相减后，再将n换成n-1，化简整理，结合等差数列的性质和定义，即可得证．
解答 证明：当n=1时，a1=S1，且2S1-a1=10．
解得a1=10，
当n＞1时，2Sn-nan=10n，
即有2Sn-1-（n-1）an-1=10（n-1）．
两式相减，可得2an-nan+（n-1）an-1=10，
将n换成n-1可得，2an-1-（n-1）an-1+（n-2）an-2=10，
即有（2-n）an+（n-1）an-1=（3-n）an-1+（n-2）an-2，
（2-n）an-2+（2-n）an=2（2-n）an-1．
即为an-2+an=2an-1．即有an-an-1=an-1-an-2=…=a2-a1．
由等差数列的定义可得，数列{an}是等差数列．
点评 本题考查数列的通项和求和之间的关系，考查等差数列的判断：运用等差中项，考查推理能力，属于中档题．
练习册系列答案
相关题目
18．设两个相互独立事件A，B都不发生的概率是$\frac{1}{9}$，则A与B都发生的概率的范围是（ ）
| A． | [0，$\frac{8}{9}$] | B． | [$\frac{1}{9}$，$\frac{5}{9}$] | C． | [$\frac{2}{3}$，$\frac{8}{9}$] | D． | [0，$\frac{4}{9}$] |
5．如图，已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，P、Q在渐近线上，PQ的中垂线过点F，O是坐标原点，若∠PFQ=Rt∠，OQ=3OP，则双曲线的离心率等于（ ）
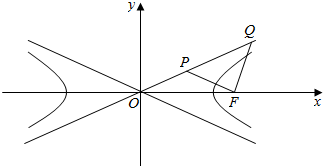
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{5}{4}$ | D． | $\frac{5}{3}$ |