题目内容
已知数列{ }成等比数列,且
}成等比数列,且 >0.
>0.
(1)若a2﹣a1=8,a3=m.
①当m=48时,求数列{ }的通项公式;
}的通项公式;
②若数列 { }是唯一的,求m的值;
}是唯一的,求m的值;
(2)若a2k+a2k﹣1+…+ak+1﹣(ak+ak﹣1+…+a1)=8,k∈N*,求a2k+1+a2k+2+…+a3k的最小值.
 }成等比数列,且
}成等比数列,且 >0.
>0.(1)若a2﹣a1=8,a3=m.
①当m=48时,求数列{
 }的通项公式;
}的通项公式;②若数列 {
 }是唯一的,求m的值;
}是唯一的,求m的值;(2)若a2k+a2k﹣1+…+ak+1﹣(ak+ak﹣1+…+a1)=8,k∈N*,求a2k+1+a2k+2+…+a3k的最小值.
解:(1)设等比数列{ }的公比为q,由题意可得q>0.
}的公比为q,由题意可得q>0.
①当m=48时,由a2﹣a1=8,a3=48 可得 ,
,
解得 ,或
,或  .
.
数列{ }的通项公式为
}的通项公式为  =8(2﹣
=8(2﹣ )
) ,或
,或
 =8(2+
=8(2+ )
)  .
.
②若数列 { }是唯一的,则
}是唯一的,则 有唯一的正数解,
有唯一的正数解,
即方程8q2﹣mq+m=0 有唯一的正数解,
由△=m2﹣32m=0 可得m=32,此时,q=2, =2n+2.
=2n+2.
(2)若a2k+a2k﹣1+…+ak+1﹣(ak+ak﹣1+…+a1)=8,k∈N*,
则有 qk(ak+ak﹣1+…+a1)﹣(ak+ak﹣1+…+a1)=8,q>1,
即 (qk﹣1)(ak+ak﹣1+…+a1)=8,
即 a1(qk﹣1)( qk﹣1+qk﹣2+qk﹣3+…q+1)=8.
∴a2k+1+a2k+2+…+a3k =a1q2k( qk﹣1+qk﹣2+qk﹣3+…q+1)=a1q2k
= =
= =8[(qk﹣1)+2+
=8[(qk﹣1)+2+ ]≥8(2+2)=32,
]≥8(2+2)=32,
当且仅当 qk﹣1= 时,等号成立,
时,等号成立,
故a2k+1+a2k+2+…+a3k的最小值为 32.
 }的公比为q,由题意可得q>0.
}的公比为q,由题意可得q>0.①当m=48时,由a2﹣a1=8,a3=48 可得
 ,
,解得
 ,或
,或  .
.数列{
 }的通项公式为
}的通项公式为  =8(2﹣
=8(2﹣ )
) ,或
,或 =8(2+
=8(2+ )
)  .
.②若数列 {
 }是唯一的,则
}是唯一的,则 有唯一的正数解,
有唯一的正数解,即方程8q2﹣mq+m=0 有唯一的正数解,
由△=m2﹣32m=0 可得m=32,此时,q=2,
 =2n+2.
=2n+2.(2)若a2k+a2k﹣1+…+ak+1﹣(ak+ak﹣1+…+a1)=8,k∈N*,
则有 qk(ak+ak﹣1+…+a1)﹣(ak+ak﹣1+…+a1)=8,q>1,
即 (qk﹣1)(ak+ak﹣1+…+a1)=8,
即 a1(qk﹣1)( qk﹣1+qk﹣2+qk﹣3+…q+1)=8.
∴a2k+1+a2k+2+…+a3k =a1q2k( qk﹣1+qk﹣2+qk﹣3+…q+1)=a1q2k

=
 =
= =8[(qk﹣1)+2+
=8[(qk﹣1)+2+ ]≥8(2+2)=32,
]≥8(2+2)=32,当且仅当 qk﹣1=
 时,等号成立,
时,等号成立,故a2k+1+a2k+2+…+a3k的最小值为 32.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
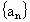 是首项a且公比q不等于1的等比数列,
是首项a且公比q不等于1的等比数列, 是其前n项和,
是其前n项和,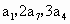 成等差数列.
成等差数列.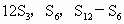 成等比数;
成等比数;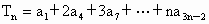 .
. 成等比数,其中k1=1,k2=2,k3=5.
成等比数,其中k1=1,k2=2,k3=5. .
.