题目内容
(三级达标校与非达标校做)
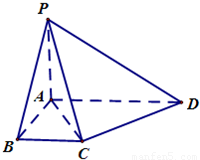
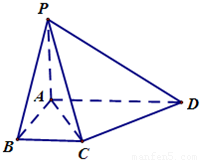
如图,在梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PA=
.
(Ⅰ) 求证:AD∥平面PBC;
(Ⅱ)求四面体A-PCD的体积.
如图,在梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PA=
| 2 |
(Ⅰ) 求证:AD∥平面PBC;
(Ⅱ)求四面体A-PCD的体积.

证明:(1)

在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC;
(Ⅱ)梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,AC=CD=
,AD=2,
因为CD⊥PC,PA⊥平面ABCD,
所以四面体A-PCD的体积就是VP-ACD,所以底面面积为:S=
×
×
=1;又PA=
是三棱锥的高.
所以VP-ACD=
S•PA=
×1×
=
.

在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC;
(Ⅱ)梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,AC=CD=
| 2 |
因为CD⊥PC,PA⊥平面ABCD,
所以四面体A-PCD的体积就是VP-ACD,所以底面面积为:S=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
所以VP-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| ||
| 3 |

练习册系列答案
相关题目
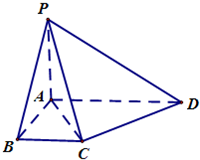 (三级达标校与非达标校做)
(三级达标校与非达标校做)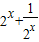 (x∈R)
(x∈R)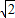 .
.
 .
.