题目内容
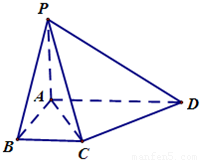
(三级达标校与非达标校做)如图,在梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PA=
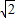 .
.(Ⅰ) 求证:AD∥平面PBC;
(Ⅱ)求四面体A-PCD的体积.
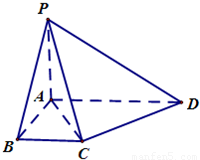
【答案】分析:(Ⅰ)直接利用直线与平面平行的判定定理,通过AD∥BC,即可证明AD∥平面PBC;
(Ⅱ)求四面体A-PCD的体积,只需转化为VP-ACD,求出底面面积与高即可求解三棱锥的体积..
解答:证明:(1) 在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,
在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,
∴AD∥平面PBC;
(Ⅱ)梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,AC=CD= ,AD=2,
,AD=2,
因为CD⊥PC,PA⊥平面ABCD,
所以四面体A-PCD的体积就是VP-ACD,所以底面面积为:S= =1;又PA=
=1;又PA= 是三棱锥的高.
是三棱锥的高.
所以VP-ACD= =
= =
= .
.
点评:本题考查直线与平面平行的判定定理的应用,几何体体积的求法,考查转化思想,计算能力.
(Ⅱ)求四面体A-PCD的体积,只需转化为VP-ACD,求出底面面积与高即可求解三棱锥的体积..
解答:证明:(1)
 在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,
在梯形ADBC中,AD∥BC,AD?平面PBC,BC?平面PBC,∴AD∥平面PBC;
(Ⅱ)梯形ADBC中,AD∥BC,AB⊥BC,AB=BC=1,AC=CD=
 ,AD=2,
,AD=2,因为CD⊥PC,PA⊥平面ABCD,
所以四面体A-PCD的体积就是VP-ACD,所以底面面积为:S=
 =1;又PA=
=1;又PA= 是三棱锥的高.
是三棱锥的高.所以VP-ACD=
 =
= =
= .
.点评:本题考查直线与平面平行的判定定理的应用,几何体体积的求法,考查转化思想,计算能力.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 (三级达标校与非达标校做)
(三级达标校与非达标校做)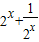 (x∈R)
(x∈R)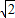 .
.