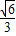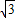题目内容
设△ABC是边长为2的等边三角形,P是△ABC内任意一点,P到三边的距离分别为d1,d2,d3,根据三角形PAB、PBC、PCA的面积之和等于△ABC的面积,可得d1,d2,d3为定值
,由此类比:P是棱长为3的正四面体ABCD内任意一点,且P到各面的距离分别为h1,h2,h3,h4,则h1+h2+h3+h4的值为( )
| 3 |
A.
| B.
| C.
| D.
|
棱长为a的正四面体ABCD的高为
a
故棱长为3的正四面体ABCD的高为
根据等积法,正四面体ABCD体积等于三棱锥P-ABC,P-ABD,P-ACD和P-BCD的体积和
而这些棱锥的底面积均是相等的
故意h1+h2+h3+h4=
故选B
| ||
| 3 |
故棱长为3的正四面体ABCD的高为
| 6 |
根据等积法,正四面体ABCD体积等于三棱锥P-ABC,P-ABD,P-ACD和P-BCD的体积和
而这些棱锥的底面积均是相等的
故意h1+h2+h3+h4=
| 6 |
故选B

练习册系列答案
相关题目
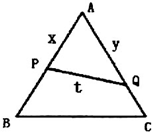 已知△ABC是边长为2的正三角形,P,Q依次是AB,AC边上的点,且线段PQ将△ABC分成面积相等的两部分,设AP=x,AQ=t,PQ=y.
已知△ABC是边长为2的正三角形,P,Q依次是AB,AC边上的点,且线段PQ将△ABC分成面积相等的两部分,设AP=x,AQ=t,PQ=y.
 ,由此类比:P是棱长为3的正四面体ABCD内任意一点,且P到各面的距离分别为h1,h2,h3,h4,则h1+h2+h3+h4的值为( )
,由此类比:P是棱长为3的正四面体ABCD内任意一点,且P到各面的距离分别为h1,h2,h3,h4,则h1+h2+h3+h4的值为( )