Question

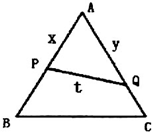已知△ABC是边长为2的正三角形，P，Q依次是AB，AC边上的点，且线段PQ将△ABC分成面积相等的两部分，设AP=x，AQ=t，PQ=y．
（1）求t关于x的函数关系式；
（2）求y的最值，并写出取得最值得条件．

Answer 1

分析：（1）利用线段PQ将△ABC分成面积相等的两部分，建立方程，即可求t关于x的函数关系式；
（2）利用余弦定理，确定函数解析式，确定x的范围，利用基本不等式，即可得出结论．

解答：解：（1）由已知得

1

2

×2×2×sin60°=2×

1

2

×t×x×sin60°，
∴t=

2

x

；
（2）由题意，y=

x2+t2-2xtcos60°

=

x2+t2-xt

=

x2+ 4 x2 -2

，
∵

0＜x≤2 0＜ 2 x ≤2

，
∴1≤x≤2，
∴x2+

4

x2

-2≥4-2=2，
当且仅当x2=

4

x2

，
即x=

2

时等号成立，
∴x=

2

时，y_min=

2

；当x=1或2时，y_max=

3

．

点评：本题考查三角形面积的计算，考查余弦定理的运用，考查基本不等式的运用，属于中档题．