题目内容
在长方体ABCD-A1B1C1D1中,M、N分别是棱BB1、B1C1的中点,若∠CMN=90°,则异面直线DA1与DM所成的角为
[ ]
A.
30°
B.
45°
C.
60°
D.
90°
答案:D
解析:
解析:
|
本题考查了异面直线所成角的求法.可以用常规法判定它们的关系,也可用坐标运算的方法. 方法一:连结DM、BC1,则MC为DM在平面B1C内的射影. MN∥BC1∥AD1,
又∵CM⊥MN,∴DM⊥MN. ∴DM⊥AD1,即AD1与DM所成角为90°. 方法二:以D1A1、D1C1、D1D所在直线为x轴、y轴、z轴建立空间直角坐标系. 设D1A1=a,D1C1=b,D1D=c, 则M(a,b, ∴ 又∵∠CMN=90°,∴ ∴a2= 又 ∴ ∴ |

练习册系列答案
相关题目

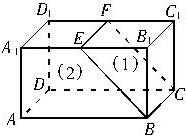 9、如图,在长方体ABCD-A1B1C1D1中,EF∥B1C1,用 平面BCFE把这个长方体分成了(1)、(2)两部分后,这两部分几何体的形状是( )
9、如图,在长方体ABCD-A1B1C1D1中,EF∥B1C1,用 平面BCFE把这个长方体分成了(1)、(2)两部分后,这两部分几何体的形状是( ) 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E、F分别为A1B1、A1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E、F分别为A1B1、A1D1的中点. 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的 (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.