题目内容
定义在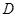 上的函数
上的函数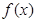 ,如果满足:对任意
,如果满足:对任意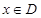 ,存在常数
,存在常数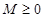 ,都有
,都有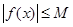 成立,则称
成立,则称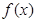 是
是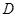 上的有界函数,其中
上的有界函数,其中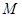 称为函数
称为函数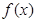 的一个上界.已知函数
的一个上界.已知函数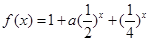 ,
,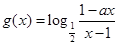 .
.
(1)若函数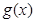 为奇函数,求实数
为奇函数,求实数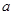 的值;
的值;
(2)在(1)的条件下,求函数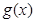 在区间
在区间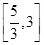 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数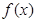 在
在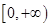 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数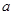 的取值范围.
的取值范围.
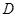 上的函数
上的函数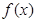 ,如果满足:对任意
,如果满足:对任意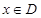 ,存在常数
,存在常数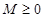 ,都有
,都有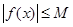 成立,则称
成立,则称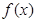 是
是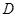 上的有界函数,其中
上的有界函数,其中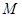 称为函数
称为函数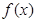 的一个上界.已知函数
的一个上界.已知函数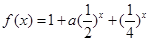 ,
,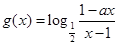 .
.(1)若函数
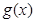 为奇函数,求实数
为奇函数,求实数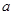 的值;
的值;(2)在(1)的条件下,求函数
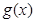 在区间
在区间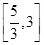 上的所有上界构成的集合;
上的所有上界构成的集合;(3)若函数
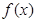 在
在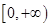 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数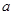 的取值范围.
的取值范围.(1) ;(2)
;(2)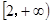 ;(3)
;(3)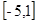 .
.
 ;(2)
;(2)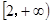 ;(3)
;(3)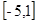 .
.试题分析:(1)因为
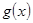 为奇函数,所以利用
为奇函数,所以利用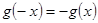 ,求出
,求出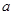 的值;(2) 在(1)的条件下,证明
的值;(2) 在(1)的条件下,证明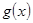 的单调性,
的单调性,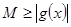 在
在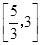 恒成立,即
恒成立,即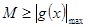 ,根据单调性,可以求出其最大值;(3)若函数
,根据单调性,可以求出其最大值;(3)若函数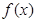 在
在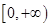 上是以3为上界的有界函数,则
上是以3为上界的有界函数,则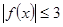 ,将函数代入,反解
,将函数代入,反解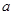 ,
,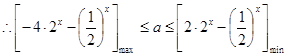 ,利用函数的单调性求出他们的最大,和最小值,就是
,利用函数的单调性求出他们的最大,和最小值,就是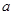 的范围.
的范围.试题解析:解:(1)因为函数
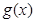 为奇函数,
为奇函数,所以
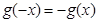 ,即
,即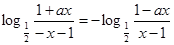 ,
,即
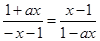 ,得
,得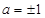 ,而当
,而当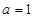 时不合题意,故
时不合题意,故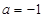 . 4分
. 4分(2)由(1)得:
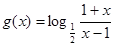 ,
,下面证明函数
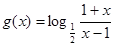 在区间
在区间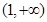 上单调递增,
上单调递增,证明略. 6分
所以函数
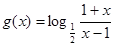 在区间
在区间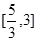 上单调递增,
上单调递增,所以函数
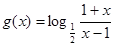 在区间
在区间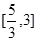 上的值域为
上的值域为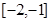 ,
,所以
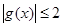 ,故函数
,故函数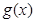 在区间
在区间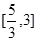 上的所有上界构成集合为
上的所有上界构成集合为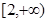 . 8分
. 8分(3)由题意知,
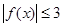 在
在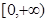 上恒成立.
上恒成立.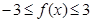 ,
,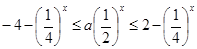 .
.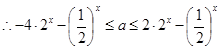 在
在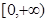 上恒成立.
上恒成立.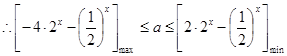 10分
10分设
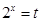 ,
,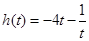 ,
,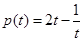 ,由
,由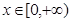 得
得 ,
,设
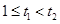 ,
,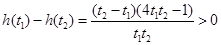 ,
,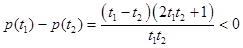 ,
,所以
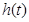 在
在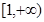 上递减,
上递减,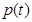 在
在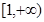 上递增, 12分
上递增, 12分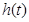 在
在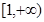 上的最大值为
上的最大值为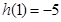 ,
,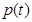 在
在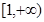 上的最小值为
上的最小值为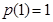 .
.所以实数
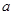 的取值范围为
的取值范围为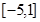 . 14分
. 14分
练习册系列答案
相关题目
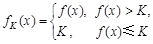 (K为给定常数),已知函数
(K为给定常数),已知函数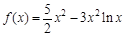 ,若对于任意的
,若对于任意的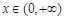 ,恒有
,恒有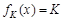 ,则实数K的取值范围为 .
,则实数K的取值范围为 .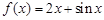 的部分图象可能是( )
的部分图象可能是( )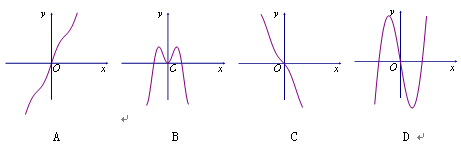
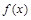 的定义域为A,若
的定义域为A,若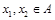 且
且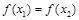 时总有
时总有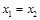 ,则称
,则称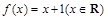 是单函数.下列命题:
是单函数.下列命题: 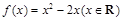 是单函数;
是单函数;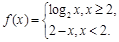 是单函数;
是单函数;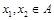 且
且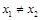 ,则
,则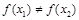 ;
; 的奇偶性、单调性均相同的是( )
的奇偶性、单调性均相同的是( )



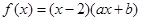 为偶函数,且在
为偶函数,且在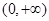 单调递增,则
单调递增,则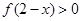 的解集为( )
的解集为( )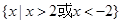

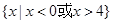

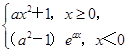 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.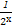 ,若f(x)=
,若f(x)=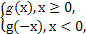 则函数f(x)在定义域内( )
则函数f(x)在定义域内( )