题目内容
已知α,β是锐角,且sinα=
思路分析:因为β∈(0,![]() ),所以2β∈(0,π).所以先求cos2β的值,然后再选用适当的三角函数求α+2β的值.
),所以2β∈(0,π).所以先求cos2β的值,然后再选用适当的三角函数求α+2β的值.
解:∵sinβ=![]() ,∴cos2β=1-2sin2β=
,∴cos2β=1-2sin2β=![]() .
.
由β∈(0,![]() )且cos2β=
)且cos2β=![]() >0,可推得2β∈(0,
>0,可推得2β∈(0,![]() ),
),
∴α+2β∈(0,π).
∴cos(α+2β)=cosαcos2β-sinαsin2β.
∵α∈(0,![]() )且sinα=
)且sinα=![]() ,
,
得cosα=![]() ,
,
又2β∈(0,![]() )且cos2β=
)且cos2β=![]() ,
,
∴sin2β=![]() .
.
∴cos(α+2β)=![]() .
.
∴α+2β=![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 ,若
,若 则
则 = 。
= 。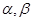 都是锐角,且
都是锐角,且 .
.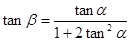 ;
;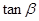 取最大值时,求
取最大值时,求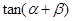 的值.
的值.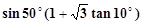 .
.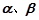 都是锐角,且
都是锐角,且 .
.