题目内容
(2013•东莞二模)已知函数f(x)=2
sinxcosx-2cos2x+1.
(1)求函数f(x)的对称轴方程及单调递增区间;
(2)在△ABC中,若f(
)=2,b=1,c=2,求a的值.
| 3 |
(1)求函数f(x)的对称轴方程及单调递增区间;
(2)在△ABC中,若f(
| A |
| 2 |
分析:(1)利用三角函数倍角公式和两角和的正弦公式可得f(x)=
sin2x-cos2x=2sin(2x-
),由对称轴方程满足2x-
=kπ+
,k∈Z即可解出;再利用正弦函数的单调性即可得出单调区间.
(2)利用三角函数的单调性和余弦定理即可得出.
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
(2)利用三角函数的单调性和余弦定理即可得出.
解答:解:(1)f(x)=
sin2x-cos2x=2sin(2x-
)
对称轴方程满足2x-
=kπ+
,k∈Z
即x=
kπ+
,k∈Z,
由2kπ-
≤2x-
≤2kπ+
得,kπ-
≤x≤kπ+
(k∈Z),
故f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z).
(2)f(
)=2,则2sin(A-
)=2⇒sin(A-
)=1,
∴A-
=
+2kπ,A=
+2kπ,k∈Z.
又0<A<π,∴A=
,
∴a2=b2+c2-2bccosA=7,∴a=
.
| 3 |
| π |
| 6 |
对称轴方程满足2x-
| π |
| 6 |
| π |
| 2 |
即x=
| 1 |
| 2 |
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
故f(x)的单调递增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
(2)f(
| A |
| 2 |
| π |
| 6 |
| π |
| 6 |
∴A-
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
又0<A<π,∴A=
| 2π |
| 3 |
∴a2=b2+c2-2bccosA=7,∴a=
| 7 |
点评:熟练掌握三角函数倍角公式、两角和的正弦公式、对称轴方程、三角函数的单调性和余弦定理是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
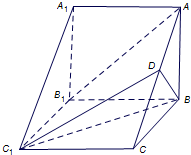 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.