题目内容

（2013•东莞二模）已知x＞0，y＞0，且
1
x
+
9
y
=1，则2x+3y的最小值为
29+6
6
29+6
6
．
分析：把
1
x
+
9
y
=1代入可得，2x+3y=（2x+3y）（
1
x
+
9
y
）=
3y
x
+
18x
y
+29，由基本不等式可得答案．
解答：解：由题意可得2x+3y=（2x+3y）（
1
x
+
9
y
）
=
3y
x
+
18x
y
+29≥2
3y
x
•
18x
y
+29=29+6
6

当且仅当
3y
x
=
18x
y
，即x=
6+
6
54
，y=
6+
6
9
时取等号，
故2x+3y的最小值为：29+6
6

故答案为：29+6
6
点评：本题考查基本不等式的应用，把
1
x
+
9
y
=1代入原式构造可利用基本不等式的情形是解决问题的关键，属基础题．
练习册系列答案
相关题目
（2013•东莞二模）设Sn为数列{an}前n项和，对任意的n∈N*，都有Sn=2-an，数列{bn}满足bn=
bn-1
1+bn-1
，b1=2a1，
（1）求证：数列{an}是等比数列，并求{an}的通项公式；
（2）求数列{bn}的通项公式；
（3）求数列{
1
an+2bn
}的前n项和Tn．
（2013•东莞二模）命题“?x∈R，x2+1≥1”的否定是（　　）
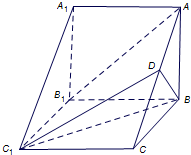（2013•东莞二模）如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．
（1）求证：AB1∥平面BC1D；
（2）若BC=3，求三棱锥D-BC1C的体积．
（2013•东莞二模）已知函数f(x)=tan(
1
3
x-
π
6
)
（1）求f（x）的最小正周期；
（2）求f(
3π
2
)的值；
（3）设f(3α+
7π
2
)=-
1
2
，求
sin(π-α)+cos(α-π)
2
sin(α+
π
4
)
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网