题目内容
16．若向量$\overrightarrow a$，$\overrightarrow b$的长度分别为3和4，夹角为120°，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的值为（ ）| A． | 5 | B． | $\sqrt{13}$ | C． | 7 | D． | $\sqrt{37}$ |
分析 根据向量模的计算和向量的数量积的运算即可求出．
解答 解：|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$||$\overrightarrow{b}$|cos$＜\overrightarrow{a}$，$\overrightarrow{b}$＞=9+16+2×3×4×（-$\frac{1}{2}$）=13，
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$，
故选：B．
点评 本题考查了向量模的计算和向量的数量积的运算，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
如图所示，正四棱柱ABCD-A1B1C1D1中，AB=λAA1，O是底面ABCD的中心，求λ的值，使得A1O⊥面BDC1．
4．已知椭圆的一个焦点与抛物线y2=4x的焦点重合，且椭圆的离心率为$\frac{\sqrt{2}}{2}$，该椭圆的方程为（ ）
| A． | $\frac{{x}^{2}}{2}+{y}^{2}=1$ | B． | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$ | C． | $\frac{{y}^{2}}{2}+{x}^{2}=1$ | D． | $\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1$ |
11．在区间[0，6]上随机取一个数x，则事件“1≤2x≤5”发生的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
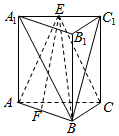如图，在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB⊥BC，$A{A_1}=AC=2，AB=\sqrt{3}$，E，F分别是A1C1，AB的中点．
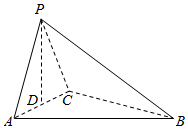如图所示，在三棱锥P-ABC中，点P在平面ABC上的射影D与AC的中点重合，已知BC=2AC=8，AB=4$\sqrt{5}$．