题目内容
已知椭圆C: +
+ =1(a>b>0)的左.右焦点为F1、F2,离心率为e.直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e.直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 =λ
=λ .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
解:(Ⅰ)因为A、B分别是直线l:y=ex+a与x轴、y轴的交点,所以A、B的坐标分别是(- ,0)(0,a).
,0)(0,a).
由 得
得 .这里c=
.这里c= .
.
所以点M的坐标是(-c, ).由
).由 =λ
=λ 得(-c+
得(-c+ ,
, )=λ(
)=λ( ,a).
,a).
即 .解得λ=1-e2.
.解得λ=1-e2.
(Ⅱ)因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,
要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即 |PF1|=c.
|PF1|=c.
设点F1到l的距离为d,
由 |PF1|═d=
|PF1|═d= =
= =c,
=c,
得 =e.
=e.
所以e2= ,于是λ=1-e2=
,于是λ=1-e2= .
.
即当λ= 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
分析:(Ⅰ)因为A、B分别是直线l:y=ex+a与x轴、y轴的交点,所以A、B的坐标分别是(- ,0)(0,a).由题设知点M的坐标是(-c,
,0)(0,a).由题设知点M的坐标是(-c, ).由
).由 =λ
=λ 得(-c+
得(-c+ ,
, )=λ(
)=λ( ,a).从而解得λ=1-e2.
,a).从而解得λ=1-e2.
(Ⅱ)因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有 |PF1|=c.由题设知当λ=
|PF1|=c.由题设知当λ= 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
点评:本题考查直线和圆锥曲线的综合问题,解题时要认真审题,仔细求解,合理地运用公式.
 ,0)(0,a).
,0)(0,a).由
 得
得 .这里c=
.这里c= .
.所以点M的坐标是(-c,
 ).由
).由 =λ
=λ 得(-c+
得(-c+ ,
, )=λ(
)=λ( ,a).
,a).即
 .解得λ=1-e2.
.解得λ=1-e2.(Ⅱ)因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,
要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即
 |PF1|=c.
|PF1|=c.设点F1到l的距离为d,
由
 |PF1|═d=
|PF1|═d= =
= =c,
=c,得
 =e.
=e.所以e2=
 ,于是λ=1-e2=
,于是λ=1-e2= .
.即当λ=
 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.分析:(Ⅰ)因为A、B分别是直线l:y=ex+a与x轴、y轴的交点,所以A、B的坐标分别是(-
 ,0)(0,a).由题设知点M的坐标是(-c,
,0)(0,a).由题设知点M的坐标是(-c, ).由
).由 =λ
=λ 得(-c+
得(-c+ ,
, )=λ(
)=λ( ,a).从而解得λ=1-e2.
,a).从而解得λ=1-e2.(Ⅱ)因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有
 |PF1|=c.由题设知当λ=
|PF1|=c.由题设知当λ= 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.点评:本题考查直线和圆锥曲线的综合问题,解题时要认真审题,仔细求解,合理地运用公式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为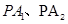 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.