题目内容
如图,在等腰梯形PDCB中,PB=3,DC=1,PD=BC=| 2 |
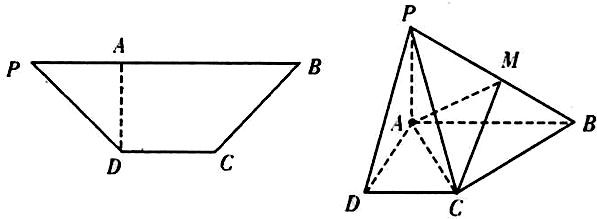
(1)求证:平面PAD⊥平面PCD;
(2)试在PB上找一点M,使截面AMC把几何体分成两部分,且VM-ACB=
| 1 |
| 3 |
(3)在(2)的条件下,判断AM是否平行于平面PCD.
分析:(1)先由平面PAD⊥平面ABCD?DC⊥平面PAD?平面PAD⊥平面PCD即可.
(2)因为S△ABC=
SABCD且VM-ACB=
VP-ABCD;所以对应高之比为
,所以可得M为PB中点.
(3)用反证法证之;若AM∥平面PCD?平面ABM∥平面PCD?与平面ABM与平面PCD有公共点P矛盾.即可.
(2)因为S△ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
(3)用反证法证之;若AM∥平面PCD?平面ABM∥平面PCD?与平面ABM与平面PCD有公共点P矛盾.即可.
解答:解:(1)证明:依题意知CD⊥AD,
又∵平面PAD⊥平面ABCD,
∴DC⊥平面PAD
又DC?平面PCD,
∴平面PAD⊥平面PCD.(4分)
(2)解:∵VM-ACB=
VP-ABCD,(6分)
设P、M到底面ABCD的距离分别为h、hM,
则
•S△ABC•hM=
•(
SABCD)•h?
•
SABCD•hM=
•(
SABCD)•h
∴hM=
h,
∴M为PB中点.(8分)
(3)∵AB∥CD,AB?平面PCD,CD?平面PCD,
∴AB∥平面PCD(10分)
若AM∥平面PCD,∵AB∩AM=A,
∴平面ABM∥平面PCD
这与平面ABM与平面PCD有公共点P矛盾
∴AM与平面PCD不平行(12分)
又∵平面PAD⊥平面ABCD,
∴DC⊥平面PAD
又DC?平面PCD,
∴平面PAD⊥平面PCD.(4分)
(2)解:∵VM-ACB=
| 1 |
| 3 |
设P、M到底面ABCD的距离分别为h、hM,
则
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴hM=
| 1 |
| 2 |
∴M为PB中点.(8分)
(3)∵AB∥CD,AB?平面PCD,CD?平面PCD,
∴AB∥平面PCD(10分)
若AM∥平面PCD,∵AB∩AM=A,
∴平面ABM∥平面PCD
这与平面ABM与平面PCD有公共点P矛盾
∴AM与平面PCD不平行(12分)
点评:本题考查平面和平面垂直的判定和性质.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直

练习册系列答案
相关题目
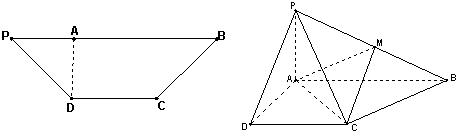
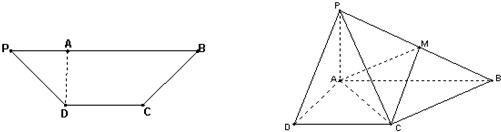
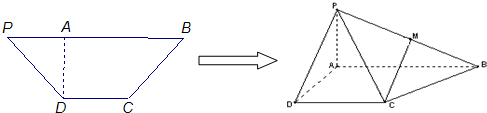
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=