题目内容
若0<a<1,下列不等关系中正确的是
- A.a0.5>a0.3
- B.0.5a>0.3a
- C.loga0.5>loga0.3
- D.0.5lga>0.3lga
B
分析:题目给出了四个选项,选项A运用指数函数的单调性比较;选项B运用幂函数单调性比较;选项C运用对数函数的单调性比较,选项D在求出lga的范围后,运用幂函数单调性比较.
解答:因为0<a<1,所以指数函数y=ax为减函数,由0.5>0.3,所以a0.5<a0.3,所以A不正确;
因为0<a<1,所以幂函数y=xa在第一象限为增函数,由0.5>0.3,所以0.5a>0.3a,所以B正确;
因为0<a<1,所以函数y=logax为定义域内的减函数,由0.5>0.3,所以loga0.5<loga0.3,所以C不正确;
因为0<a<1,所以lga<0,则函数y=xlga在第一象限为减函数,由0.5>0.3,所以0.5lga<0.3lga,所以D不正确.
故选B.
点评:本题考查了不等式的大小比较,考查了基本初等函数的单调性,是基础题.
分析:题目给出了四个选项,选项A运用指数函数的单调性比较;选项B运用幂函数单调性比较;选项C运用对数函数的单调性比较,选项D在求出lga的范围后,运用幂函数单调性比较.
解答:因为0<a<1,所以指数函数y=ax为减函数,由0.5>0.3,所以a0.5<a0.3,所以A不正确;
因为0<a<1,所以幂函数y=xa在第一象限为增函数,由0.5>0.3,所以0.5a>0.3a,所以B正确;
因为0<a<1,所以函数y=logax为定义域内的减函数,由0.5>0.3,所以loga0.5<loga0.3,所以C不正确;
因为0<a<1,所以lga<0,则函数y=xlga在第一象限为减函数,由0.5>0.3,所以0.5lga<0.3lga,所以D不正确.
故选B.
点评:本题考查了不等式的大小比较,考查了基本初等函数的单调性,是基础题.

练习册系列答案
相关题目
下列四个命题中,不正确的是( )
A、若0<a<
| ||||
B、若0<a<1则
| ||||
C、若实数x,y满足y=x2则log2(2x+2y)的最小值是
| ||||
| D、若a,b∈R则a2+b2+ab+1>a+b |
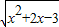 的单调减区间是(-∞,-1)
的单调减区间是(-∞,-1) 则cos(1+a)<cos(1-a)
则cos(1+a)<cos(1-a)
