题目内容
设S是实数集R的真子集,且满足下列两个条件:①1不属于S;②若a∈S,则
| 1 | 1-a |
问:(Ⅰ)若2∈S,则S中一定还有哪两个数?
(Ⅱ)集合S中能否只有一个元素?说明理由.
分析:(1)若2∈S,则
∈s即-1∈s;又根据题意又有
∈s.即
∈s.始终根据定义求解.
(2)若a∈S,则
∈S,集合S中只有一个元素,根据元素互异性要求则必有a=
即a2-a+1=0有解.
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)若a∈S,则
| 1 |
| 1-a |
| 1 |
| 1-a |
解答:解:(Ⅰ)若2∈S,则
∈s即-1∈s;又根据题意又有
∈s.即
∈s.
∴若2∈S,s中至少还有两个元素-1,
;
(Ⅱ)若a∈S,则
∈S,根据元素互异性的要求,s中只有一个元素,则应该满足
a=
即a2-a+1=0有解.显然此方程无解.
∴不可能.
答:(1)若2∈S,s中一定还有两个元素-1,
;
(2)集合S中不可能只有一个元素.
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
∴若2∈S,s中至少还有两个元素-1,
| 1 |
| 2 |
(Ⅱ)若a∈S,则
| 1 |
| 1-a |
a=
| 1 |
| 1-a |
即a2-a+1=0有解.显然此方程无解.
∴不可能.
答:(1)若2∈S,s中一定还有两个元素-1,
| 1 |
| 2 |
(2)集合S中不可能只有一个元素.
点评:集合中的元素具有互异性.这是往往容易忽视的.

练习册系列答案
相关题目
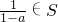 ,
,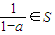 ,
,