题目内容
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.


(1)当0<t≤1时,
如图,设直线x=t与△OAB分别交于C、D两点,则|OC|=t,
又
| |CD| |
| |OC| |
| |BE| |
| |CE| |
| ||
| 1 |
| 3 |
| 3 |
∴f(t)=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(2)当1<t≤2时,
如图,设直线x=t与△OAB分别交于M、N两点,则|AN|=2-t,
又
| |MN| |
| |AN| |
| |BE| |
| |AE| |
| ||
| 1 |
| 3 |
| 3 |
∴f(t)=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
(3)当t>2时,f(t)=
| 3 |
综上所述f(t)=
|


练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
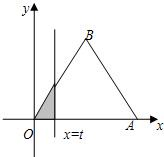 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.
如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t). 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式. (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为: