题目内容
 如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.
如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.分析:根据图象,分0≤t≤
,
<t≤1两种情况进行讨论:当0≤t≤
时,阴影部分图形为三角形,面积可表示;当
<t≤1时,阴影部分图形为三角形与一梯形,面积可转化为求三角形面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由图知,①当0≤t≤
时,y=f(t)=
t•
t=
t2;
②当
<t≤1时,y=f(t)=
×
×
+[
×
×
-
(1-t)•
(1-t)]=
+[
-
(1-t)2]=
-
(1-t)2;
故y=f(t)=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
②当
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 8 |
| ||
| 8 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
故y=f(t)=
|
点评:本题考查函数解析式的求解及常用方法,实际问题中,定义域要考虑其实际意义.

练习册系列答案
相关题目
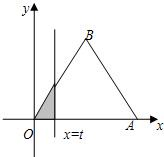 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t). 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式. (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为: